Increasing and Decreasing Functions Through Graphs and Differentiation
Explore how to determine whether a function is increasing or decreasing by analyzing graphs and using differentiation. Practice finding values of x for which a function is increasing or decreasing, and understand the concept of stationary points. Enhance your grasp of gradients and their significance in analyzing functions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
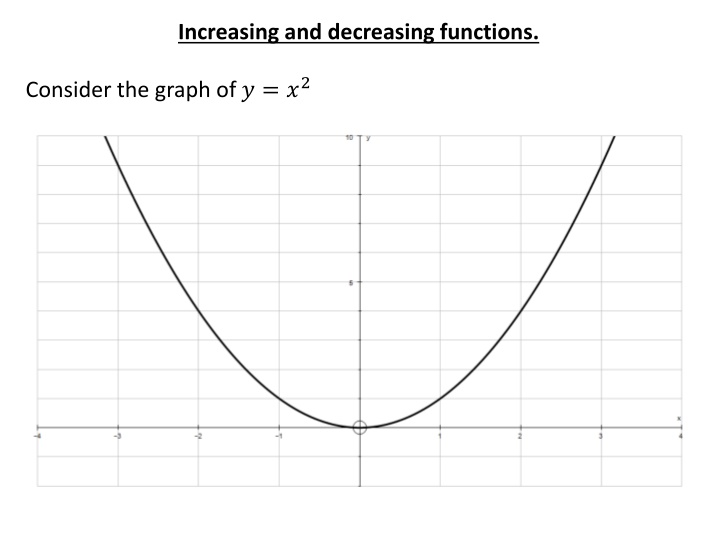
Increasing and decreasing functions. Consider the graph of ? = ?2
To determine whether the value of a function is increasing or decreasing, we use differentiation to evaluate the gradient. ? ? = ?2 EG:
Find the values of x for which f(x) is an increasing function: 1) ? ? = 3?2+ 8? + 2 2) ? ? = 4? 3?2 3) ? ? = 5 8? 2?2 Find the values of x for which f(x) is decreasing: 4) ? ? = ?2 9? If you finish quickly, sketch the graph of ? = ?(?). What does your answer tell you about the graph?
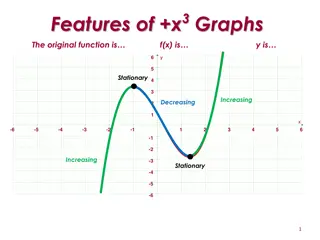
A function may have more than one set of values for which it is increasing or decreasing. Consider the function ? ? = ?3+ 3?2
1) ? ? = 2?3 15?2+ 36? increasing? 2) ? ? = 2?3 3?2 12? increasing? 3) ? ? = ?3 27? + 1 decreasing? 4) ? ? = 3?4 20?3+ 36?2+ 12 increasing?
Starter Increasing and Decreasing Functions Find the set of values for ?: 1) ? ? = 2?2+ 8? 11 decreasing? ? < ? 2) ? ? = 2?3+ 3?2 12? + 10 decreasing? ? < ? < ? 3) ? ? = ?3 3?2 24? 9 increasing? ? < ? and ? > ?
Activity: Gradients Susan Wall STEM website (login required) https://www.stem.org.uk/resources/elibrary/resource/34073/propertie s-functions
Stationary Points Stationary points occur when the gradient of a function is zero. Consider again the function ? ? = ?3+ 3?2
Practice questions Find the coordinates of the stationary points on each curve: 1) ? = ?3 ?2 ? + 1 2) ? = ?(?2 4? 3) 3) ? = ?2+54 ? 1 2(? 6) 4) ? = ?
To determine the nature of stationary/turning points, we use the second derivative. At the stationary point : ?2? ??2< 0 ? ?? ? ????? ??????? ?2? ??2> 0 ? ?? ? ????? ??????? (?2? ??2= 0 ????3? ??3 0 ?? ? ????? ?? ?????????)
Use calculus to find the coordinates of the stationary points of each curve. Determine the nature of the stationary points. 1) ? = ?3 3?2 24? 2) ? = 3?2+ 45? 75 ?3 3) ? = 2?3 24? 4) ? = ? 22(? 1)
Use calculus to find the coordinates of the stationary points of each curve. Determine the nature of the stationary points. 1)? = ?3 3?2 24? 4, 80 ???????, 2,28 ??????? 2)? = 3?2+ 45? 75 ?3 5,100 ???????, 3, 156 ??????? 3)? = 2?3 24? 2, 32 ???????, 2,32 ??????? 4 3, 4 27 ???????, 4)? = ? 22(? 1) 2,0 ???????
Activity: Floppy Hair Underground Maths https://undergroundmathematics.org/calculus-of-powers/floppy-hair