Infinite Geometric Series and Sigma Notation
Discover how to find the sum of infinite geometric series and represent series using sigma notation in mathematics. Explore examples and solutions for various series.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
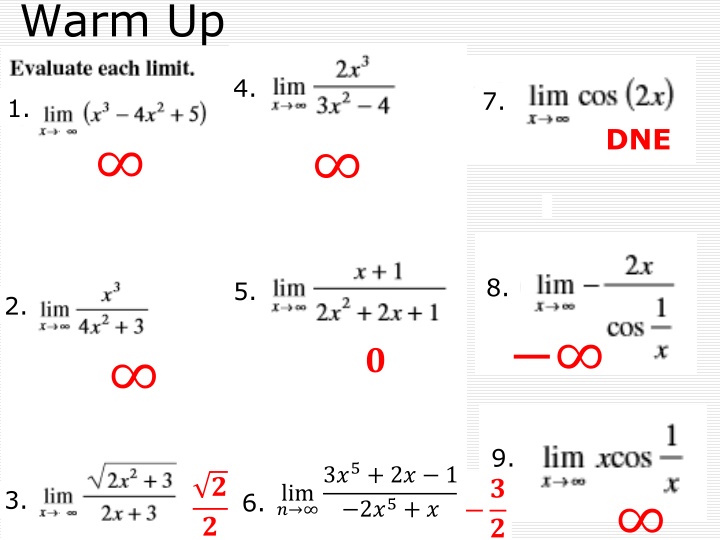
Warm Up 4. 7. 1. DNE 8. 5. 2. ? 9. 3?5+ 2? 1 2?5+ ? ? ? lim ? 3. 6. ? ?
13.5 Sums of Infinite Series Objective To find the sum of an infinite geometric series. n 1 2 1 4 1 8 1 1 2 + + + + + + . 16 n 1 2 1 4 1 8 1 1 2 = + + + + + n S 16
13.5 Sums of Infinite Series Sum of an infinite Geometri r c Serie s If 1, the infinite geometric series + + + + + 2 n t t r t r t r 1 1 1 1 t = converges to the s um . 1 S 1 r If 1 and 0, then the series diverge s. r t 1
13.5 Sums of Infinite Series Find the sum of the infinite geometric series. 9 6 4 + r 1 . 6 2 3 = = = 9 and , t r 1 9 t 9 2 7 = = = 1 . S ( ) 1 1 2/ 3 5 r
13.5 Sums of Infinite Series The repeating decimal 0.45 can be written as the infinite series 0.45 0.0045 0.000045 + What is the sum of this series? + + = = 0.45 and t r 0.01 t r 1 0.45 1 0.01 0.45 .99 5 = = = = 1 S 1 11
Classwork 1. Find the sum of each series: a. 1 +1 3+1 1 27+ b. 1 2 1 4+1 1 16+ 9+ 8 c. 1 + .1 + .01 + .001 + d. 1 + 3 + 9 + 27 + 2. Express 0.3333 as an infinite geometric series. Find the sum.
Classwork 1. Find the sum of each series: a. 1 +1 3+1 1 27+ ?1 1 ? b. 1 2 1 4+1 1 16+ 9+ 8 1 = 1 =? a. = S = 1 1 2 3 ? 3 1 2 1 2 3 2 ?1 =? b. S = = = 1 ? 1 1 ? 2
Classwork 1. Find the sum of each series: c. 1 + .1 + .01 + .001 + d. 1 + 3 + 9 + 27 + ?1 1 = 1 =?? c. S = = 1 ? 1 .1 .9 ? ? = 3,Diverges d.
Classwork 2. Express 0.3333 as an infinite geometric series. Find the sum. .3 + .03 + .003 + .0003 + ?1 .3 = .3 =? S = = 1 ? 1 .1 .9 ?
13.6 Sigma Notation Objective To represent series using sigma notation. 100 = + + + + 2 2 2 2 2 1 2 3 100 k = 1 k = 2 The sum for 1 to 10 0 of . k k Index Summand Limits of Summation
SUMMATION NOTATION This number tells us when to stop (the last integer to sub in). This is the formula to sub into 5 ( ) = k + + + This sign means to sum up each of the terms in the sequence 3 3 2 k ( ) 2 1 5 ( ) 2 3 3 11 + ( ) 2 5 3 17 + 1 + + + 8 14 This number tells us what integer to start subbing in to create the terms in a sequence ( ) 2 4 3 + ( ) 2 2 3 + = 55 Often we want to sum the terms in a sequence so summation notation is a short-hand way express this.
Summation Notation Ex: Evaluate the following sum: 4 ( ) = i + 2 3 i 1 Sol: ( 1 = i 4 ) ( 3 = ) ( 3 + ) ( + ) ( + ) + + + + + 2 2 1 2 2 3 2 3 3 2 4 3 i = + + + 5 7 9 11 = 32
13.6 Sigma Notation 1 ? 2 = j = 1 1/2 1/4 1/8 ... + + + + 0 j t 1 1/2 = = = 1 2 S 1 1 r
13.6 Sigma Notation Index Try It: n 1 2 5 = ? n= 1 Summand sum( MATH 2nd List seq( OPS 2nd List ( ) x 1/2 , ,1,5,1 ( ( sum seq x Ans Frac 11/32
Classwork j 4 1 ( ) = = k 1 j Write in expanded form. 1. 2. 12 k 2 j Express the series in sigma notation. 3. 4 + 9 + 16 + 25 + 36 4. 1 2+2 3+3 4+4 5 6. 1 3+1 1 27+ 1 81+ 5. 3 + 6 + 9 + + 300 9+ Evaluate. k 2 15 50 ( ) 8. 5 32 sin n k 7. = = 7 1 k
Classwork j 4 1 ( ) = = k 1 j Write in expanded form. 1. 2. 12 k 2 j 4 1 =? ?+? ?+? ?+? = k 1. 12 k ? j ( ) = 1 = 2 12+3 13+4 14+5 15+ j 2. 2 j = ? ? + ? ? +
Classwork Express the series in sigma notation. 3. 4 + 9 + 16 + 25 + 36 4. 1 2+2 = k 3+3 4+4 k 5 6 4 = k 2 k + 1 k 2 1 6. 1 3+1 1 27+ 1 81+ 5. 3 + 6 + 9 + + 300 9+ k 100 = k 3 k k 3 1 = 1
Classwork Evaluate. 2 50 8. 7. = k 15 sin k ( ) 5 32 n = 1 k 7 7. = ??? ??? ??? 5? 32,?,7,15,1 8. ??? ??? ??? ? ? 2 ,?,1,50,1= ?
Homework Page 502 #1-9 odds, #23-27 odds Page 508 #1-19 odds






















