Influence Line Construction for Reaction, Shear, and Moment in Structural Analysis

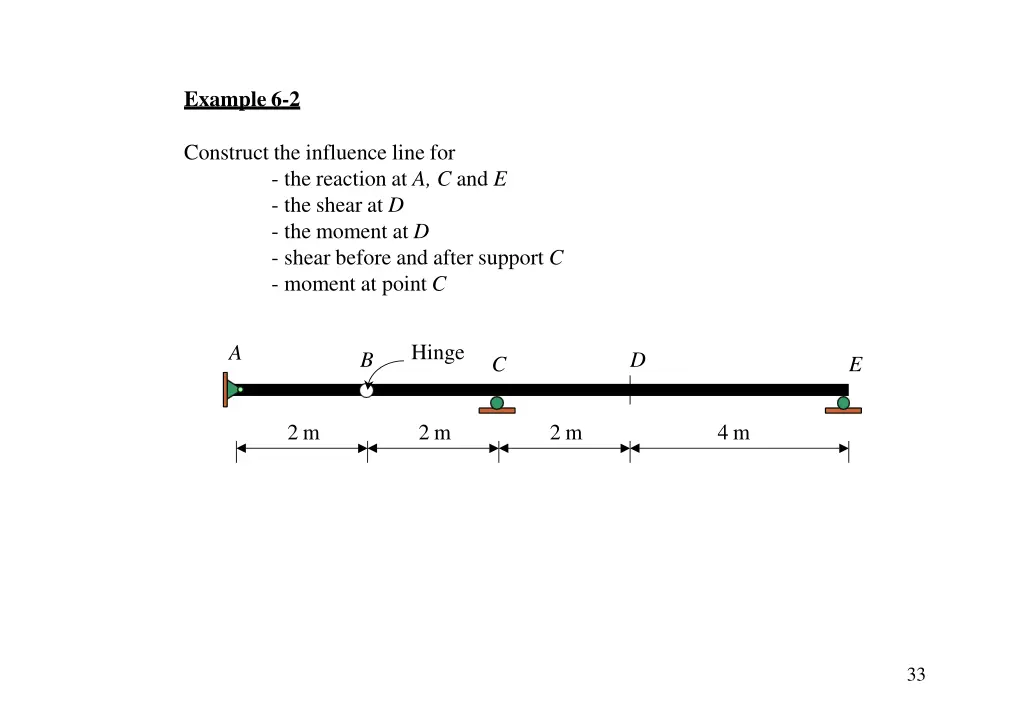
Example 6-2 Construct the influence line for - the reaction at A, C and E - the shear at D - the moment at D - shear before and after support C - moment at point C Hinge A B D C E 2 m 2 m 2 m 4 m 33

SOLUTION B D C E A 2 m 2 m 2 m 4 m RA 1 RA x 34

B D E C A 2 m 2 m 2 m 4 m RC 8/6 1 RC 4/6 x 35

A B D C E 2 m 2 m 2 m 4 m RE 1 2/6 RE x -2/6 36

VD A B D C E VD 2 m 2 m 2 m 4 m 1 4/6 2/6 VD = 1 x sE= 1/6 = -1 sC= 1/6 -2/6 sE= sC 37

Or using equilibrium conditions: 1 Hinge A B D C E 2 m 2 m 2 m 4 m 1 x VD VD 4 m 4 m MD MD RE RE VD= 1 -RE VD= -RE 1 2/6 RE x -2/6 4/6 2/6 VD x -2/6 38

MD MD A B C E D 2 m 2 m 2 m 4 m (2)(4)/6 = 1.33 4 D= C+ E= 1 2 MD C= 4/6 2/6 = E x -1.33 39

Or using equilibrium conditions: 1 Hinge A B D C E 2 m 2 m 2 m 4 m 1 x VD VD 4 m 4 m MD MD RE RE MD= -(4-x)+4RE MD= 4RE 1 2/6 RE x -2/6 8/6 MD x -8/6 40

VCL A C E B D VCL 2 m 2 m 2 m 4 m VCL x -1 -1 41

Or using equilibrium conditions: 1 A B D C E 2 m 2 m 2 m 4 m 1 MB MB VCL VCL RA RA VCL= RA - 1 V = RA CL 1 RA x VCL x -1 -1 42

VCR A C E B D VCR 2 m 2 m 4 m 2 m 1 0.667 0.333 VCR x 43

Or using equilibrium conditions: 1 A B D C E 2 m 2 m 2 m 4 m 1 MC MC VCR VCR RE RE VCR= -RE VCR= 1 -RE 1 2/6=0.33 RE x -2/6 = -0.333 1 0.667 0.333 VCR x 44

A MCCMC B D E 2 m 2 m 2 m 4 m MC x 1 -2 45

Or using equilibrium conditions: A 1 B D C E 2 m 2 m 2 m 4 m 1 x' MC MC 6 m 6 m VCR VCR RE RE MC= 6RA x' MC= 6RE 1 2/6=0.33 RE x -2/6 = -0.333 MC x 1 -2 46

Example 6-3 Construct the influence line for - the reaction at A and C - shear at D, E and F - the moment at D, E and F Hinge A B D C E F 2 m 2 m 2 m 2 m 2 m 2 m 47

SOLUTION B D C E F A 2 m 2 m 2 m 2 m 2 m 2 m RA 1 1 RA 0.5 x -0.5 -1 48

A B D E F C RC 2 m 2 m 2 m 2 m 2 m 2 m 2 1.5 1 0.5 RC x 49

VD A B C E F D VD 2 m 2 m 2 m 2 m 2 m 2 m 1 1 VD = 0.5 x = -0.5 -1 50

VE A B D C F E VE 2 m 2 m 2 m 2 m 2 m 2 m 0.5 = VE 1 x = -0.5 -0.5 -1 51

VF A B D C E F VF 2 m 2 m 2 m 2 m 2 m 2 m 1 = VF x = 52

A B D C E F MD MD 2 m 2 m 2 m 2 m 2 m 2 m 2 MD 1 x D = 1 -1 -2 53

MEC BME A D E F 2 m 2 m 2 m 2 m 2 m 2 m (2)(2)/4 = 1 = 1 ME E x B= 0.5 C = 0.5 -1 -2 54

ME CME A B D E F 2 m 2 m 2 m 2 m 2 m 2 m MF x F= 1 -2 55

Example 6-4 Determine the maximum reaction at support B, the maximum shear at point C and the maximum positive moment that can be developed at point C on the beam shown due to - a single concentrate live load of 8000 N - a uniform live load of 3000 N/m - a beam weight (dead load) of 1000 N/m A C B 4 m 4 m 4 m 56

SOLUTION 8000 N 3000 N/m 1000 N/m A B C 4 m 4 4 m m RB 1.5 1 0.5 0.5(12)(1.5) = 9 x = (1000)(9) + (3000)(9) + (8000)(1.5) (RB)max = 48000 N = 48 kN 57

8000 N 3000 N/m 3000 N/m 1000 N/m A B C 4 m 4 m 4 m VC 0.5 0.5(4)(0.5)= 1 x 0.5(4)(-0.5)= -1 0.5(4)(-0.5)= -1 -0.5 -0.5 = (1000)(-2+1) + (3000)(-2) + (8000)(-0.5) (VC)max = -11000 N = 11 kN 58

8000 N 3000 N/m 1000 N/m A B C 4 m 4 m 4 m MC 2 +(1/2)(8)(2) =8 x (1/2)(4)(2) = 4 -2 = (8000)(2) + (3000)(8) + (8-4)(1000) (MC)max positive = 44000 N m = 44 kN m 59