Insights on IA Work and Sykefravær Management
The content delves into the nuances of IA work and sykefravær management, highlighting the necessity for proper implementation and understanding of workplace laws. It underscores the evolving landscape of employee care and the potential impacts on future sykefravær rates.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
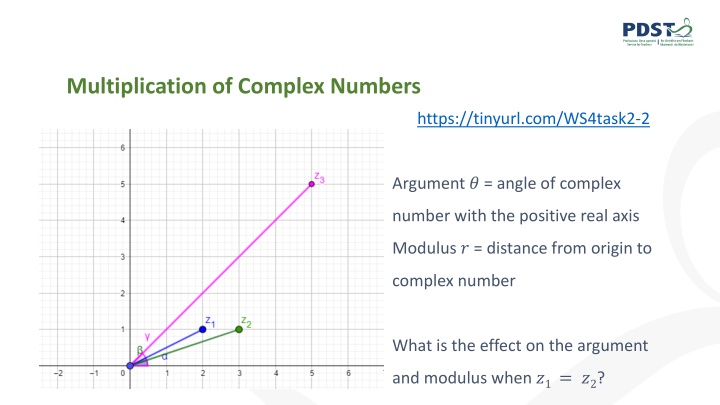
Multiplication of Complex Numbers https://tinyurl.com/WS4task2-2 https://tinyurl.com/WS4task2-2 Argument ? = angle of complex number with the positive real axis Modulus ? = distance from origin to complex number What is the effect on the argument and modulus when ?1= ?2?
From Rectangular Form to Polar Form Argument ? = angle of complex number with the positive real axis Modulus ? = distance from origin to complex number Write ? = 1 + ? in Polar Form
From Rectangular Form to Polar Form ?(???? + ? ????) Argument ? ??? ? = ? = Modulus ? ? = ? = From rectangular to polar form 1 + ? = 2(??? 11 ? 4 12+ 12 2 ? ? ? 4+ 1 ??? 4) Write ? = 1 + ? in Polar Form
Multiplication of Complex Numbers The effect of multiplying a complex number by itself: Multiplication z x z = z2 z x z x z = z3 z x z x z x z = z4 z x z x z x z x z = z5 zn Argument (angle ) Modulus (r) Doubled Squared Tripled Cubed Multiplied by 4 Multiplied by itself 4 times Multiplied by 5 Multiplied by itself 5 times Multiplied by n Multiplied by itself n times De Moivre s theorem: ?? = ?? (cos?? + ?sin? )
De Moivres Theorem: ?? Find ? + ??? = ?? (cos?? + ? sin? ) From rectangular to polar form ? ? 1 + ? = 2(??? 4+ 1 ??? 4) 10??? 1 + ?10= 10 ? ? 2 4+ ? ??? 4 ? 10???10 1 + ?10= ? ? 2 4 + ? ???10 4 1 + ?10= 32(cos 5? 5? 2+ ?sin 2) 1 + ?10= 32(0 + 1?) 1 + ?10= 0 + 32? Find ? = 1 + ?10