Introduction to Logarithmic Functions
In this introduction to logarithmic functions, learn about the inverse relationship with exponential functions, graphical reflections, algebraic processes, and more. Explore the characteristics, domain, and range of exponential functions and how to find the inverse of an exponential function both graphically and algebraically.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Bellwork Find the value of x in each exponential equation.
Introduction to Logarithmic Introduction to Logarithmic Functions Functions Section 6.3
Introduction to Logarithmic Functions Introduction to Logarithmic Functions In 1st semester, you were introduced to inverse functions. Inverse functions is the set of ordered pair obtained by interchanging the x and y values. f(x) f-1(x)
Introduction to Logarithmic Functions Introduction to Logarithmic Functions Inverse functions can be created graphically by a reflection on the y = x axis. f(x) f-1(x)
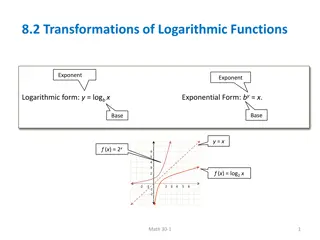
Introduction to Logarithmic Functions A logarithmic function is the inverse of an exponential function Exponential functions have the following characteristics: Domain: ARN Range: {y > 0}
Introduction to Logarithmic Functions Let us graph the exponential function y = 2x Table of values:
Introduction to Logarithmic Functions Introduction to Logarithmic Functions Let us find the inverse the exponential function y = 2x Table of values:
Introduction to Logarithmic Functions When we add the function f(x) = 2x to this graph, it is evident that the inverse is a reflection on the y = x axis f-1(x) f(x) f(x) f-1(x)
Introduction to Logarithmic Functions Next, you will find the inverse of an exponential algebraically Write the process in your notes base y = ax Interchange x y x = ay We write these functions as: x = ay exponent x = ay y = logax y = logax exponent base
Introduction to Logarithmic Functions y = ax Exponential Function Inverse of the Exponential Function y log x Logarithmic Form
Introduction to Logarithmic Functions Example 1) Write the following into logarithmic form: a) 33 = 27 b) 45 = 256 c) 27 = 128 ANSWERS d) (1/3)x=27 ANSWERS
Introduction to Logarithmic Functions Example 1) Write the following into logarithmic form: a) 33 = 27 log327=3 b) 45 = 256 log4256=5 c) 27 = 128 log2128=7 log1/327=x d) (1/3)x=27
Introduction to Logarithmic Functions Example 2) Write the following into exponential form: a) log264=6 b) log255=1/2 c) log81=0 ANSWERS d) log1/39=-2 ANSWERS
Introduction to Logarithmic Functions Example 2) Write the following into exponential form: 26 = 64 a) log264=6 b) log255=1/2 251/2 = 5 80 = 1 c) log81=0 (1/3)-2 = 9 d) log1/39=-2
Two special logarithm values that you should learn to recognize. let b be a positive real number such that b 1. (Take note)
Types of logarithms Types of logarithms: (Take Note) : (Take Note) logarithms to base 10 are called common logarithms logarithms to base 2 are called binary logarithms logarithms to base e are called natural logarithms Logarithmic Identities: logx = b x b x = b b log x
Introduction to Logarithmic Functions Example 3) Find the value of x for each example: a) log1/327 = x b) log5x = 3 c) logx(1/9) = 2 d) log3x = 0
Introduction to Logarithmic Functions Example 3) Find the value of x for each example: a) log1/327 = x b) log5x = 3 53 = x x = 125 (1/3)x = 27 (1/3)x = (1/3)-3 x = -3 c) logx(1/9) = 2 d) log3x = 0 x2 = (1/9) x = 1/3 30 = x x = 1
Introduction to Logarithmic Functions Scientific calculators can perform logarithmic operations. Your calculator has a LOG button. This button represents logarithms in BASE 10 or log10 Example 4) Use your calculator to find the value of each of the following: a) log101000 = 3 b) log 50 c) log -1000 = Out of Domain = 1.699