Introduction to Triangles - Classifying, Theorems, and Angles
This educational material covers the classification of triangles by angles and sides, the sum of interior angles theorem, exterior angles, remote interior angles, and related theorems. It includes examples, definitions, and matching exercises to enhance understanding.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
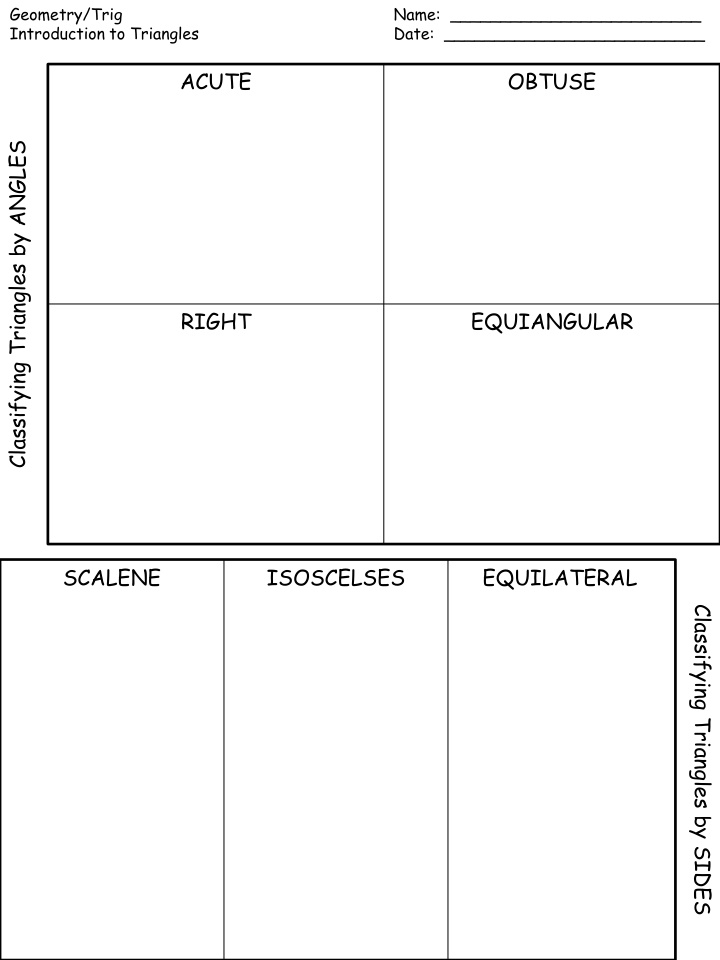
Geometry/Trig Introduction to Triangles Name: _________________________ Date: __________________________ ACUTE OBTUSE Classifying Triangles by ANGLES RIGHT EQUIANGULAR SCALENE ISOSCELSES EQUILATERAL Classifying Triangles by SIDES
B Vertices of ABC: _________________ Sides of ABC: ___________________ Angles of ABC: ___________________ C A Theorem: the three interior angles of a triangle sum to _________. x = ______ m A = _______ m B = _______ m C = _______ Example 1: m A = 56 m B = ____ m C = 82 Example 2: m A = 3x + 5 m B = x - 4 m C = 2x + 11 Given: ___________________________ Prove: ___________________________ Statements Reasons 1. 2. 1. 2. 3. 4. 5. 6. 3. 4. 5. 6. Corollary: The acute angles in a right triangle are ____________________. Given: ________________________ Prove: ________________________ Statements Reasons 1. 2. 3. 4. 5. 6. 1. 2. 3. 4. 5. 6.
Exterior Angle of a Triangle: An angle that forms a ____________________ with an interior angle of a triangle. In ABC, ____________, is an exterior angle. Remote Interior Angles: the two angles of the triangle that are not ____________ to a specific exterior angle. With respect to exterior 4, the remote interior angles are ___________ and _____________. Identify the remote interior angles for each exterior angle. 2 _______________ 6 ________________ 1 _______________ 5 ________________ 7 & 9 are remote interior angles for the exterior angles ________ Theorem: The exterior angle is equal to the sum of the two remote interior angles. Given: ABC Prove: m 1 + m 2 = m 4 Statements Reasons 1. 1. 2. 2. 3. 3. 4. 4. 5. 5. Given: ________________________________ x = ____, m 1 = ____, m 2 = ____, m 3 = ____, m 4 = ____, m 5 = ____ Given: ________________________________ x = ____, m 1 = ____, m 2 = ____, m 3 = ____, m 4 = ____, m 5 = ____
Match the definitions with the correct vocab term. Then turn to page 93 and copy down the diagrams for each. A triangle one right angle (measures exactly 90 degrees). The other two angles are acute and are complementary. A triangle with three congruent sides. A triangle with three acute angles (all three angle measures are below 90 degrees). A triangle with NO congruent sides. A triangle with three congruent angles. The three angles all measure 60 degrees. These triangles are also classified as acute. A triangle with two congruent sides. A triangle with one obtuse angle (a angle that measures over 90 and under 180). The other two angles are acute.