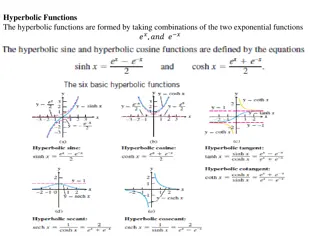
Inverse Relations and Functions Lesson 7
Students will learn about finding inverse functions, solving equations for simple functions with inverses, verifying functions through composition, reading values from graphs or tables, and creating invertible functions from non-invertible ones. Key vocabulary includes inverse functions and the horizontal line test.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Inverse Relations and Functions Unit 1 Lesson 7
Inverse Relations and Functions Students will be able to: Find inverse functions. Solve an equation of the form ? ? = c for a simple function ? that has an inverse and write an expression for the inverse. Verify by composition that one function is the inverse of another. Read values of an inverse function from a graph or a table, given that the function has an inverse. Produce an invertible function from a non-invertible function by restricting the domain.
Inverse Relations and Functions Key Vocabulary: Inverse function One-to one function Horizontal line test
Inverse Relations and Functions The inverse of a relation is a relation obtained by reversing or swapping the coordinates of each ordered pair in the relation. If the relation is described by an equation in the variables ? and ?, the equation of the inverse relation is obtained by replacing every ? in the equation with ? and every ? in the equation with ?.
Inverse Relations and Functions If ? ? represents a function of ?, the inverse of the function is represented by the symbol ? ?? . ? ? ?? ? ?.
Inverse Relations and Functions Sample Problem 1: Find the inverse of each relation given as a set of ordered pairs. a. ? ? ? ? ? ? ? ? ? ?
Inverse Relations and Functions Sample Problem 1: Find the inverse of each relation given as a set of ordered pairs. a. ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
Inverse Relations and Functions Sample Problem 1: Find the inverse of each relation given as a set of ordered pairs. b. ? ? ? ? ? ? ? ?? ? ?
Inverse Relations and Functions Sample Problem 1: Find the inverse of each relation given as a set of ordered pairs. b. ? ? ? ? ? ? ? ?? ? ? ? ? ?? ? ? ? ? ? ? ?
Inverse Relations and Functions Horizontal Line Test A function ? has an inverse function ? ? if and only if each horizontal line intersects the graph of the function in at most one point. If a function passes the horizontal line test, then it is said to be one-to-one, because no ?-value is matched with more than one ?-value and no ?-value is matched with more than one ? -value. .
Inverse Relations and Functions Horizontal Line Test If a function ? is one-to-one, it has an inverse function ? ? such that the domain of ? is equal to the range of ? ?, and the range of ? is equal to the domain of ? ?. .
Inverse Relations and Functions Sample Problem 2: Use a horizontal line test to determine whether of the graph of each function is a one-to-one function. a. ? ? = ?? ? y 5 4 3 2 1 x -5 -4 -3 -2 -1 1 2 3 4 5 -1 -2 -3 -4 -5
Inverse Relations and Functions Sample Problem 2: Use a horizontal line test to determine whether of the graph of each function is a one-to-one function. a. ? ? = ?? ? y 5 Because we can draw at least one horizontal line that intersects the graph more than once, ? ? = ?? ? is not a one-to-one function. Therefore the inverse of ? ? = ?? ? is a relation, but not a function. 4 3 2 1 x -5 -4 -3 -2 -1 1 2 3 4 5 -1 -2 -3 -4 -5
Inverse Relations and Functions Sample Problem 2: Use a horizontal line test to determine whether of the graph of each function is a one-to-one function. b. ? ? = ??+ ? y 5 4 3 2 1 x -5 -4 -3 -2 -1 1 2 3 4 5 -1 -2 -3 -4 -5
Inverse Relations and Functions Sample Problem 2: Use a horizontal line test to determine whether of the graph of each function is a one-to-one function. b. ? ? = ??+ ? y 5 Because every horizontal line we draw intersects the graph only once, ? ? = ??+ ? is a one-to-one function. Therefore the inverse of ? ? = ??+ ? is a function. 4 3 2 1 x -5 -4 -3 -2 -1 1 2 3 4 5 -1 -2 -3 -4 -5
Inverse Relations and Functions Step by Step Procedure to Find the Inverse of ? ? 1. Determine whether the function has an inverse by checking to see if it is one-to-one. 2. Replace ? ? with ?. 3. Interchange ? and ?. 4. Solve for ?.
Inverse Relations and Functions Step by Step Procedure to Find the Inverse of ? ? 5. Replace ? with ? ?? . 6. State any restrictions on the domain of ? ?? . Sometimes only part of the function you find algebraically may be the inverse function of ?. Therefore, be sure to analyze the domain of ? when finding ? ?.
Inverse Relations and Functions The graphs of the function and the inverse function are reflections across the line ? = ?.
Inverse Relations and Functions Sample Problem 3: Find the inverse function, state any restrictions on its domain and then graph the function and its inverse. ? ? = ?? ? a.
Inverse Relations and Functions Sample Problem 3: Find the inverse function, state any restrictions on its domain and then graph the function and its inverse. ? ? = ?? ? ? = ?? ? ? = ?? ? ? + ? = ?? ? + ? ? + ? = ?? ? + ? ? ? = ( , ) ? = ( , ) a. ? ?? =? + ? ? = ( , ) ? = ( , ) = ? ?
Inverse Relations and Functions Sample Problem 3: Find the inverse function, state any restrictions on its domain and then graph the function and its inverse. ? ?? =? + ? ? ? = ?? ? a. ? y 5 4 3 2 1 x -5 -4 -3 -2 -1 1 2 3 4 5 -1 -2 -3 -4 -5
Inverse Relations and Functions Sample Problem 3: Find the inverse function, state any restrictions on its domain and then graph the function and its inverse. ? ? = ? ?? b.
Inverse Relations and Functions Sample Problem 3: Find the inverse function, state any restrictions on its domain and then graph the function and its inverse. ? = ( , ) ? = ( , ) ? ? = ? ?? ? = ? ?? ? = ? ?? ? b. ?? = ? ?? ?? = ? ? ?? + ? = ? ? + ? ? = ( , ) ? = ( , ) ?? + ? = ? ? ?? = ?? + ?
Inverse Relations and Functions Sample Problem 3: Find the inverse function, state any restrictions on its domain and then graph the function and its inverse. ? ?? = ?? + ? ? ? = ? ?? b. y 5 4 3 2 1 x -5 -4 -3 -2 -1 1 2 3 4 5 -1 -2 -3 -4 -5
Inverse Relations and Functions Sample Problem 3: Find the inverse function, state any restrictions on its domain and then graph the function and its inverse. ? ? = ? ? + ? c.
Inverse Relations and Functions Sample Problem 3: Find the inverse function, state any restrictions on its domain and then graph the function and its inverse. c. ? ? = ? ? + ? ? = ? ? + ? ? = ?, ? = ?, ? = ? ? + ? ??= ?? ??= ? ? + ? ??= ?? + ? ?? ? ? ? = ?, ? = ?, ? ? + ? ? ?? =?? ? ? ? = ? ?
Inverse Relations and Functions Sample Problem 3: Find the inverse function, state any restrictions on its domain and then graph the function and its inverse. ? ?? =?? ? ? ? = ? ? + ? ? ? c. ? y 5 4 3 2 1 x -5 -4 -3 -2 -1 1 2 3 4 5 -1 -2 -3 -4 -5
Inverse Relations and Functions Compositions of Inverse Functions Two functions, ? and ?, are inverse functions if and only if: ? ?(?) = ?, for every ? in the domain of ?(?) and ? ?(?) = ?, for every ? in the domain of ? ? .
Inverse Relations and Functions Sample Problem 4: Show algebraically that ?and ? are inverse functions. ? ? =? + ? ? ? = ?? ? a. ?
Inverse Relations and Functions Sample Problem 4: Show algebraically that ?and ? are inverse functions. ? ? =? + ? ? ? = ?? ? a. ? ? ? ? = ? ? ? ? ? + ? ? ? ? ? = ? ? ? ? ? = ? + ? ? ? ? ? = ?
Inverse Relations and Functions Sample Problem 4: Show algebraically that ?and ? are inverse functions. ? ? =? + ? ? ? = ?? ? a. ? =? ? + ? =?? ? + ? =?? ? = ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
Inverse Relations and Functions Sample Problem 4: Show algebraically that ?and ? are inverse functions. ? ? = ??+ ?? + ? ? ? ? ? = ? + ? ? b.
Inverse Relations and Functions Sample Problem 4: Show algebraically that ?and ? are inverse functions. ? ? = ??+ ?? + ? ? ? ? ? = ? + ? ? b. ? ? ? = ? ? + ? ? ??+ ?? + ? + ? ? ? ? ? = ??+ ?? + ? ? ? ? ? = ? + ?? ? ? ? ? = ? ? ? ? ? ? = ? + ? ? = ?
Inverse Relations and Functions Sample Problem 4: Show algebraically that ?and ? are inverse functions. ? ? = ??+ ?? + ? ? ? ? ? = ? + ? ? b. ?+ ? ? ? + ? ? ? ? = ? ? ?+ ? ( ? + ? ?) + ? ? ? ? = ? + ? ? ? ? ? = ? + ? ? ? + ? + ? + ? ? + ? ?? + ? ? ? ? = ?