Inverse Z-Transform Methods: Partial Fractions Analysis
Learn about finding the inverse of Z-transform using partial fraction method for complex functions with multiple order poles. Understand the process step-by-step with practical examples and solutions provided.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
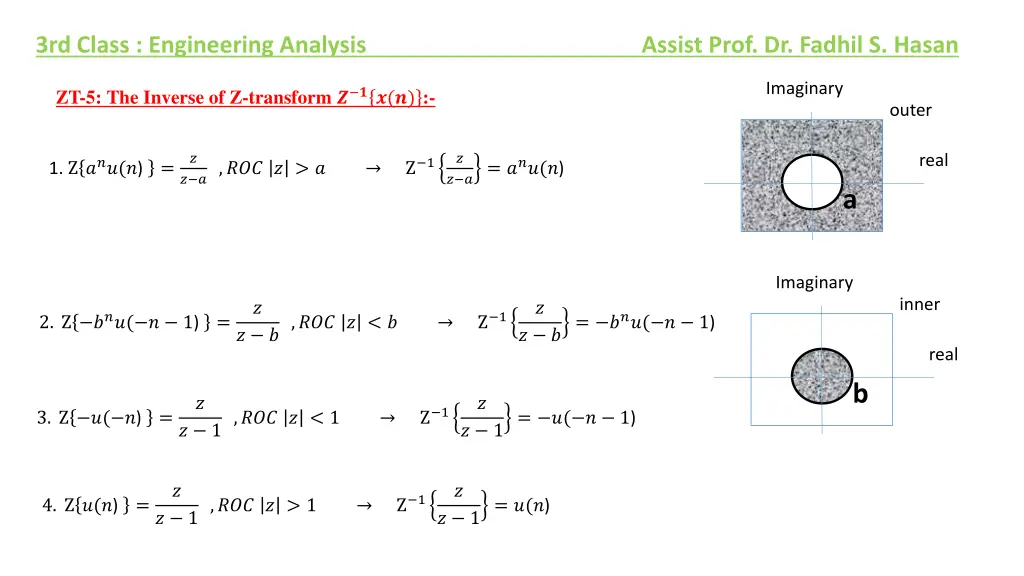
3rd Class : Engineering Analysis Assist Prof. Dr. Fadhil S. Hasan Imaginary ZT-5: The Inverse of Z-transform ? ??(?) :- outer real ? ? 1. ???(?) = 1 ? ?= ???(?) ? ? ,??? ? > ? a Imaginary inner ? ? 2. ???( ? 1) = 1 = ???( ? 1) ? ? ,??? ? < ? ? ? real b ? ? 1 3. ?( ?) = ? 1 ,??? ? < 1 = ?( ? 1) ? 1 ? ? 1 4. ?(?) = ? 1 ,??? ? > 1 = ?(?) ? 1
11 = ?(n) 5. ?(?) = 1 ,??? ??? ? ? ? (? 1)2 ROC: ? > 1 1 (? 1)2=n u(n) 6. ??(?) = There are many methods to find the inverse of Z-transform 1. Partial fraction method i. Distinct poles X ? ? ?1 ?2 ?? = + + + ? ?1 ? ?2 ? ?? X ? ? ??= lim ? ??? ?? 1 Example : Find ? ? for X ? = 1 1.5? 1+0.5? 2 for the following ROC's: ?) ? > 1 , b) ? < 0.5 and c) 0.5 < ? < 1
Solution: ?2 ?2 1.5? + 0.5 X ? ? ?1 ?2 X ? = = (? 1)(? 0.5)= ? 1+ ? ? 0.5 ? ? ?1= lim = 2, ?2= lim = 1 ? 0.5 ? 1 ? 1 ? 0.5 X ? ? 2 1 ? ? = ? 1 ? 0.5, X ? = 2 ? 1 ? 0.5 a. a. ??? ? > ? ? ? = 2? ? 0.5??(?)
?.??? ? < 0.5 ? ? = 2? ? 1 + 0.5??( ? 1 ) ?.??? 0.5 < ? < 1 ? ? = 2? ? 1 0.5??(? )
ii. Multiple order poles 1 Example: Find ? ? ) for X ? = (1+? 1)(1 ? 1)2 ?3 1 Solution: X ? = (1+? 1)(1 ? 1)2= (?+1)(? 1)2 ?2 ) X(? ? ?12 ? 12+ ?11 ? 1+ ?3 = ? + 1) ? 12= ? + 1 ?2 =1 ?12= lim 2, ? + 1 ? 1 2? ? + 1 ?2 ? + 12 =3 ?11= lim 4 ? 1 ?2 ? 12=1 ?3= lim 4 ? 1
1 2? 3 4? ? 1+ 1 4? ? + 1 X(?) = ? 12+ ?(?) =1 2??(?) +3 4?(?) +1 4 1??(?) Notes: ???(?)is a right hand sequence (causal or positive time sequence). ???( ? 1)is a left hand sequence (anti-causal or negative time sequence). Example : Find the inverse Z-transform of ?2+ ? (? 0.5)3(? 0.25) ??? ? ? ??? ? >1 X ? = 2 Solution: ?13 ?12 ?11 ?4 X ? ? ? + 1 = ? 0.53+ ? 0.52+ + = ? 0.53(? 0.25 ? 0.5 ? 0.25 )
? + 1 ? 0.25 ? 0.25 ? 1 ? 0.252 ?13= lim = 6, ?12= lim = 20 ? 0.5 ? 0.5 ?2 ??2 ?11=1 ? + 1 ? 0.25 =1 ? ?? 1.25 ? 0.252 2!lim ? 0.5 2.5 ? 0.25 ? 0.254= 80 2!lim ? 0.5 =1 2lim ? 0.5 ? + 1 ? 0.53= 80 ?4= lim ? 0.25 6? 20? 80? ? 0.5 80? X ? = ? 0.53 ? 0.52+ ? 0.25 ? 2 ? 1 ? ? x ? = 6? ? 1 1 2 1 2 1 2 1 4 ? ? 20? ? ? + 80 ? ? 80 ?(? 2
Notes: At ?? ??? ? > ? ? ? 1 ? ?= ???(?). ? ? 1 (? ?)2= ??? 1?(?) ? ?(? 1) ? 1 ?? 2?(?) (? ?)3= 2! ? ? ? 1 ? 2 (? ?+2) In general ? 1 ?? ?+1?(?) (? ?)?= (? 1)! HW: Using the partial fraction method to find ?(?) for ?(?2 4?+5) (? 3)(? 1)(? 2) ??? ??? ? (?) 2 < ? < 3,(?) ? > 3,(?) ? < 1 1. X ? = ?3+2?2 ? 0.52(?+3 4)??? ??? ? >3 2. X ? = 4