Iterative Methods for System Solutions
Discover the Gauss Jacobi and Gauss Seidel iterative methods for solving systems of equations in mathematics. Learn about their convergence conditions and step-by-step solution approaches with examples. Dive into the world of iterative methods prepared by Dr. L. Benedict Michael Raj, an Associate Professor at St. Joseph's College in Trichy.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
ITERATIVE METHODS Prepared by, Dr. L. Benedict Michael Raj Associate Professor Department of Mathematics, St. Joseph s College(Autonomous), Trichy
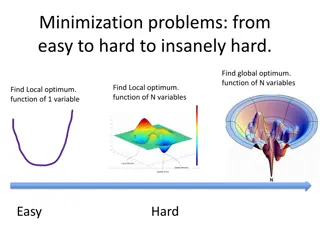
Iterative Methods This method is also called as indirect method. There are two types of iterative methods. (1)Gauss Jacobi Method (2)Gauss Seidel Method The condition for convergence Gauss Jacobi & Gauss Seidel methods is given by the following rule. of the system, the absolute value of the largest coefficient is greater than the sum of the absolute values of all the remaining coefficients. The process of iteration will converge if each equation
Gauss Jacobi Method Problem Solution consider the given system as We write the equations in the form x=1/8(20+3y-2z) y=1/11(33-4x+z) z=1/12(35-6x-3y) solve the equations by Jacobi iteration method the system. 8x-3y+2z=20 6x+3y+12z=35 4x+11y-z=33 8x-3y+2z=20 4x+11y-z=33 6x+3y+12z=35
We start from an approximation x = y = x X=1/8(20+3y-2z) Y=1/11(33-4x+z) Z=1/12(35-6x-3y) I.NO 1. 2.5 3 2.9166 2. 2.8958 2.3560 0.9166 3. 3.1543 2.0303 0.8797 4. 3.0419 1.9329 0.8319 5. 3.0168 1.9696 0.9127 6. 3.0104 1.9859 0.9158 7. 3.0157 1.9885 0.9149 8. 3.0169 1.9865 0.9116
X=1/8(20+3y-2z) Y=1/11(33-4x+z) Z=1/12(35-6x-3y) I.NO 9. 3.0170 1.9857 0.9115 10. 3.0167 1.9857 0.9116 11. 3.0167 1.9858 0.9118 12. 3.0167 1.9858 0.9118 Therefore, from the 11th &12th iterations, the values x, y, z are same correct to four decimal places. Stopping at this stage, we get x=3.0167 y=1.9858 z=0.9118
Gauss Seidel Method stage of iteration are used in preceeding to the next stage of iteration, this method is more rapid in convergence than Gauss Jacobi method. * This is modification of Gauss Jacobi method. * The current values of the unknowns at each Problem Solve the equations by Gauss Seidel method. 8x-3y+2z=20 6x+3y+12z=35 4x+11y-z=33
Solution consider the given system as 8x-3y+2z=20 4x+11y-z=33 6x+3y+12z=35 we write the equations in the form x=1/8(20+3y-2z) y=1/11(33-4x+z) z=1/12(35-6x-3y) x = y = z = 0
Z=1/12(35-6x-3y) I.NO X=1/8(20+3y-2z) Y=1/11(33-4x+z) 1. 2.5 2.0909 1.1439 2. 2.9981 2.0137 0.9141 3. 3.0266 1.9825 0.9077 4. 3.0165 1.9856 0.9120 5. 3.0166 1.9859 0.9118 6. 3.0167 1.9858 0.9118 7. 3.0167 1.9858 0.9118
since at the 6th & 7th iterations the values of x, y, z are the same. They are x=3.0167 y=1.9858 z=0.9118