Kinematics and Projectile Motion in Mechanics

Introduction In this chapter you will extend the knowledge of kinematics from M1 You will use the SUVAT equations to solve problems in 2D where a particle has vertical and horizontal motion (commonly referred to as projectiles) You will also see how to solve problems involving variable velocities and accelerations, and how calculus from Core Maths fits into Mechanics!

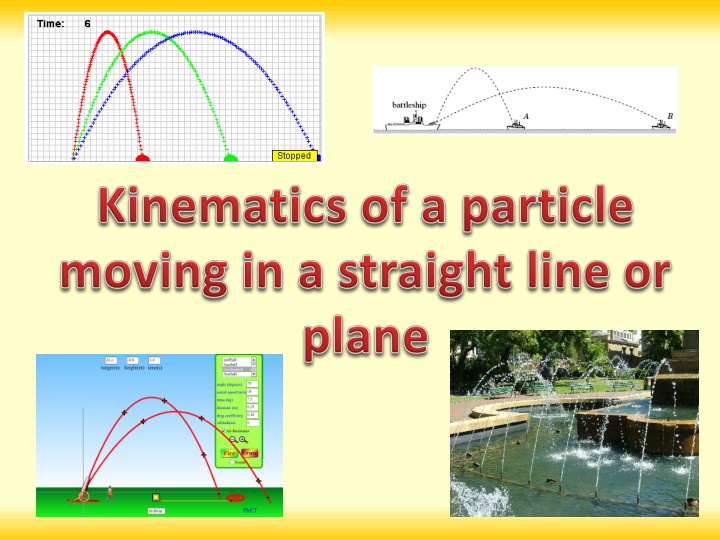
Kinematics of a particle moving in a straight line or plane u ms-1 You can use the constant acceleration formulae for a projectile moving in a vertical plane When a particle is projected with initial speed u, at an angle to the horizontal, it moves along a symmetrical curve The speed u is known as the speed of projection u ms-1 uSin ms-1 The angle is known as the angle of projection (or angle of elevation) of the particle uCos ms-1 The initial projection speed can be resolved into two components as shown to the right Any particle projected at an angle will have an initial horizontal and vertical speed 1A

Kinematics of a particle moving in a straight line or plane You can use the constant acceleration formulae for a projectile moving in a vertical plane u ms-1 uSin ms-1 When a particle is projected with initial speed u, at an angle to the horizontal, it moves along a symmetrical curve uCos ms-1 The horizontal speed will be constant as there is no acceleration in this direction The speed u is known as the speed of projection ?????????? ???????? = ?????????? ????? ???? The angle is known as the angle of projection (or angle of elevation) of the particle The vertical speed will change over time because of the acceleration due to gravity (a = 9.8ms-2) The initial projection speed can be resolved into two components as shown to the right Greatest height Range 1A

Kinematics of a particle moving in a straight line or plane Start with a diagram! 28 You can use the constant acceleration formulae for a projectile moving in a vertical plane 28sin30 30 A particle P is projected from a point O on a horizontal plane with speed 28ms-1, and with angle of elevation 30 . After projection, the particle moves freely under gravity until it strikes the plane at a point A. O A 28cos30 The greatest height will be reached when the vertical velocity is 0 (as the particle stops moving up and starts moving down) Resolve vertically and use SUVAT Find: ? =? ? = 28???30 ? = 0 ? = 9.8 ? =? a) The greatest height above the plane reached by P ?2= ?2+ 2?? Sub in values 10? (0)2= (28???30)2+2( 9.8)(?) Calculate terms b) The time of flight of P 0 = 196 19.6? Rearrange c) The distance OA 19.6? = 196 Calculate 1A ? = 10?

Kinematics of a particle moving in a straight line or plane Start with a diagram! 28 You can use the constant acceleration formulae for a projectile moving in a vertical plane 28sin30 30 A particle P is projected from a point O on a horizontal plane with speed 28ms-1, and with angle of elevation 30 . After projection, the particle moves freely under gravity until it strikes the plane at a point A. O A 28cos30 The time of flight of the particle will be when its vertical displacement is 0 (ie it is at the same height it started at) Resolve vertically and use SUVAT (again) ? = 0 ? = 28???30 ? =? ? = 9.8 ? =? Find: ? = ?? +1 2??2 a) The greatest height above the plane reached by P Sub in values 0 = (28???30)(?) +1 2( 9.8)(?2) 10? Work out terms b) The time of flight of P 0 = 28????30 4.9?2 Factorise 2.9? 0 = ?(28???30 4.9?) c) The distance OA Either part could be 0 Work out the second possibility The answer of 0 corresponds to the particle s starting position. The value 2.9 is the time it takes to hit the ground again ? = 0 ?? 28???30 4.9? = 0 ? = 2.9 1A

Kinematics of a particle moving in a straight line or plane Start with a diagram! 28 You can use the constant acceleration formulae for a projectile moving in a vertical plane 28sin30 30 A particle P is projected from a point O on a horizontal plane with speed 28ms-1, and with angle of elevation 30 . After projection, the particle moves freely under gravity until it strikes the plane at a point A. O A 28cos30 The distance OA will be based on the horizontal projection speed (which is constant) We can use the time of flight calculated in part b) ?????????? ???????? = ?????????? ????? ???? Find: ?????????? ???????? = 28???30 2.9 a) The greatest height above the plane reached by P ?????????? ???????? = 69? (2??) 10? b) The time of flight of P 2.9? c) The distance OA 69? 1A

Kinematics of a particle moving in a straight line or plane Start with a diagram! 20 You can use the constant acceleration formulae for a projectile moving in a vertical plane 30m A ball is thrown horizontally, with speed 20ms-1, from the top of a building of height 30m. As the ball is projected horizontally, there is no initial velocity vertically Resolving vertically (with downwards as the positive direction) The ball must travel 30m to hit the ground ? = 30 ? = 0 ? =? Find: a) The time the ball takes to reach the ground ? = 2.5 ? = 9.8 ? =? b) The distance between the bottom of the building and the point where the ball strikes the ground ? = ?? +1 2??2 Sub in values 30 = (0)(?) +1 2?(9.8)?2 Work out terms 30 = 4.9?2 Calculate the positive value 2.5 = ? (2sf) 1A

Kinematics of a particle moving in a straight line or plane Start with a diagram! 20 You can use the constant acceleration formulae for a projectile moving in a vertical plane 30m A ball is thrown horizontally, with speed 20ms-1, from the top of a building of height 30m. Find: ?????????? ???????? = ?????????? ????? ???? ?????????? ???????? = 20 2.5 a) The time the ball takes to reach the ground ? = 2.5 ?????????? ???????? = 49? (2sf) b) The distance between the bottom of the building and the point where the ball strikes the ground Make sure you use the exact value for t rather than the rounded on from part a)! ? = 49? 1A

Kinematics of a particle moving in a straight line or plane Start with a diagram! V You can use the constant acceleration formulae for a projectile moving in a vertical plane ???? =4 Vsin 3 O ???? =4 Vcos 42.5m 5 A particle is projected from a point O with speed Vms-1 at an angle of elevation , where tan = 4/3. The point O is 42.5m above the horizontal plane. The particle strikes the plane 5 seconds after it is projected. ???? =3 5 A Resolving vertically using the information given (taking upwards as positive) The ball will be 42.5m lower after 5 seconds a) Show that V = 20ms-1 ? = 42.5 ? = ???? ? =? ? = 9.8 ? = 5 b) Find the distance between O and A ? = ?? +1 2??2 Find the values of Sin and Cos first, by labelling a triangle where Tan = 4/3 (That is, opposite = 4 and adjacent = 3) Sub in values 42.5 = (???? )(5) +1 2( 9.8)(52) Calculate terms (use sin = 4/5) Hyp 42.5 = 4? 122.5 5 Use Pythagoras Theorem to find the missing side Remember Sin = opp/hyp and Cos = adj/hyp Add 122.5 4 Opp 80 = 4? Divide by 4 3 1A 20 = ? Adj

Kinematics of a particle moving in a straight line or plane Start with a diagram! V You can use the constant acceleration formulae for a projectile moving in a vertical plane ???? =4 Vsin 3 O ???? =4 Vcos 42.5m 5 A particle is projected from a point O with speed Vms-1 at an angle of elevation , where tan = 4/3. The point O is 42.5m above the horizontal plane. The particle strikes the plane 5 seconds after it is projected. ???? =3 5 A 60m ?????????? ???????? = ?????????? ????? ???? a) Show that V = 20ms-1 V = 20 ?????????? ???????? = ???? 5 b) Find the distance between O and A 3 5 ?????????? ???????? = 20 5 Make sure you read the question we want the distance OA, not just the horizontal distance travelled! ?????????? ???????? = 60? 1A

Kinematics of a particle moving in a straight line or plane Start with a diagram! V You can use the constant acceleration formulae for a projectile moving in a vertical plane ???? =4 3 O ???? =4 42.5m 5 A particle is projected from a point O with speed Vms-1 at an angle of elevation , where tan = 4/3. The point O is 42.5m above the horizontal plane. The particle strikes the plane 5 seconds after it is projected. ???? =3 5 A 60m Use Pythagoras Theorem to calculate the distance a) Show that V = 20ms-1 V = 20 b) Find the distance between O and A Distance = 74m 42.52+ 602 = 74? (2sf) 1A

Kinematics of a particle moving in a straight line or plane Start with a diagram! You can use the constant acceleration formulae for a projectile moving in a vertical plane 15m 35 35Sin30 30 A particle is projected from a point O with speed 35ms-1 at an angle of elevation of 30 . The particle moves freely under gravity. 35Cos30 Resolving vertically, taking upwards as positive Find the length of time for which the particle is 15m or more above O ? = 15 ? = 35???30 ? =? ? = 9.8 ? =? ? = ?? +1 We want to find the times that the particle is exactly at 15m. There will be 2 of these, once as the particle is travelling up, and once as it is travelling down. 2??2 Sub in values 15 = (35???30)(?) +1 2( 9.8)(?2) Work out each term 15 = 35????30 4.9?2 ? = 4.9 Rearrange to a quadratic form ? = 35???30 4.9?2 35????30 + 15 = 0 ? = 15 This will be difficult to factorise so we should use the quadratic formula hence we need a, b and c 1A

Kinematics of a particle moving in a straight line or plane Start with a diagram! You can use the constant acceleration formulae for a projectile moving in a vertical plane 15m 35 35Sin30 30 A particle is projected from a point O with speed 35ms-1 at an angle of elevation of 30 . The particle moves freely under gravity. 35Cos30 ? = ? ?2 4?? Find the length of time for which the particle is 15m or more above O 2? ( 35???30)2 (4 4.9 15) 2(4.9) ? =35???30 We want to find the times that the particle is exactly at 15m. There will be 2 of these, once as the particle is travelling up, and once as it is travelling down. ? = 1.43 ?? 2.14 ??????? (2??) The difference between these times will be the time spent above 15m Subtract the smallest from the biggest ? = 4.9 ? = 35???30 Time above 15m = 0.71 seconds (remember to use exact answers) ? = 15 1A

Kinematics of a particle moving in a straight line or plane u You can use the constant acceleration formulae for a projectile moving in a vertical plane uSin A particle is projected from a point with speed u and an angle of elevation , and moves freely under gravity. When the particle has moved a horizontal distance x, its height above the point of projection is y. Show that: ? = ????? ??2 2?2(1 + ???2?) uCos Finding the height in terms of t Resolving vertically (upwards as positive) Use g to represent acceleration and y to represent the height above the point of projection ? = ? ? = ???? ? =? ? = ? ? = ? ? = ?? +1 2??2 In this type of question you need to form equations for the height, y, in terms of the time, t, as well as the horizontal distance, x, in terms of the time, t. Sub in values from SUVAT ? = (?????)(?) +1 2( ?)(?2) Tidy up ? = ?????? 1 The equations can then be combined to eliminate t 2??2 We now have an expression for the height in terms of u, t and ? = ?????? 1 2??2 1A

Kinematics of a particle moving in a straight line or plane u You can use the constant acceleration formulae for a projectile moving in a vertical plane uSin A particle is projected from a point with speed u and an angle of elevation , and moves freely under gravity. When the particle has moved a horizontal distance x, its height above the point of projection is y. Show that: ? = ????? ??2 2?2(1 + ???2?) uCos Finding the horizontal distance in terms of t ?????????? ???????? = ?????????? ????? ???? Sub in values (remember x is to be used to represent the horizontal distance) ? = ????? ? ? = ?????? In this type of question you need to form equations for the height, y, in terms of the time, t, as well as the horizontal distance, x, in terms of the time, t. The equations can then be combined to eliminate t ? = ?????? 1 2??2 ? = ?????? 1A

Kinematics of a particle moving in a straight line or plane Divide by cos2 ???2? + ???2? 1 ???2? + 1 ???2? You can use the constant acceleration formulae for a projectile moving in a vertical plane ? = ?????? 1 ? = ?????? 2??2 Divide by ucos ? ?????= ? A particle is projected from a point with speed u and an angle of elevation , and moves freely under gravity. When the particle has moved a horizontal distance x, its height above the point of projection is y. Show that: ? = ????? ??2 2?2(1 + ???2?) ? = ?????? 1 2??2 ???? 1 Replace t with the expression above Group the first set of terms, square the bracket Cancel u s on the first term. Sin/Cos = Tan Group terms except for Cos on the second 2 ? ? ? = ? 2? ????? ????? ?2 ? =?????? ????? 1 2? ?2???2? Now we have equations for y and x. ? = ????? ??2 1 The final answer we want has no t terms, so this is an indication that you have to eliminate t from the equations 2?2 ???2? 1/cos = sec ? = ????? ??2 2?2???2? The final answer is written as y = , so it looks like we should rearrange the x equation and substitute it into the y equation Use the trig identity above to replace sec ? = ????? ??2 2?2(???2? + 1) 1A

Kinematics of a particle moving in a straight line or plane ? = ????? ??2 You can use the constant acceleration formulae for a projectile moving in a vertical plane 2?2(1 + ???2?) Sub in the values we know 8 = 32???? 9.8(32)2 2(28)2(1 + ???2?) Calculate the large fraction A particle is projected from a point A on a horizontal plane, with initial speed 28ms-1 and an angle of elevation . The particle passes through a point B, which is 8m above the plane and a horizontal distance of 32m from A 8 = 32???? 6.4(1 + ???2?) Multiply out the bracket Rearrange to a quadratic form 8 = 32???? 6.4 + 6.4???2? 6.4???2? + 32???? 14.4 = 0 Find the two possible values of , giving your answers to the nearest degree. You can solve this like a quadratic by using the quadratic formula (Use the formula we have just calculated) ? = 6.4 ? = 32 ? = 14.4 ? = ????? ??2 2?2(1 + ???2?) 1A

Kinematics of a particle moving in a straight line or plane 6.4???2? + 32???? 14.4 = 0 You can use the constant acceleration formulae for a projectile moving in a vertical plane ? = 6.4 ? = 32 ? = 14.4 ???? = ? ?2 4?? A particle is projected from a point A on a horizontal plane, with initial speed 28ms-1 and an angle of elevation . The particle passes through a point B, which is 8m above the plane and a horizontal distance of 32m from A 2? Sub in values 322 (4 6.4 14.4) 2(6.4) ???? = 32 Calculate each possibility Use inverse Tan (and round answers) ???? = 0.5 ?? ???? = 4.5 Find the two possible values of , giving your answers to the nearest degree. ? = 27 ?? ? = 77 There will be two possibilities here: (Use the formula we have just calculated) ? = ????? ??2 2?2(1 + ???2?) B If a projectile passes through point B, there are two possible angles it could have been launched through A 1A

Kinematics of a particle moving in a straight line or plane (5i + 8j) 8j You can use the constant acceleration formulae for a projectile moving in a vertical plane A 5i A ball is struck by a racket at a point A which is 2m above horizontal ground. Immediately after being struck, the ball has velocity (5i + 8j) ms-1, where i and j are unit vectors horizontally and vertically respectively. 2m B You can use the vectors in each direction as the initial velocities Resolve vertically to find the greatest height After being struck, the ball travels freely under gravity until is strikes the ground at a point B, as shown. Find: ? =? ? = 8 ? = 0 ? = 9.8 ? =? ?2= ?2+ 2?? a) The greatest height above ground reached by the ball ? = 5.3? Sub in values (0)2= (8)2+2( 9.8)? Work out terms b) The speed of the ball as it reaches B 0 = 64 19.6? Calculate s Careful the ball starts at a height of 2m, so this must be added on! ? = 3.3? c) The angle the velocity of the ball makes with the ground as the ball reaches B ? = 5.3? 1A

Kinematics of a particle moving in a straight line or plane (5i + 8j) 8j You can use the constant acceleration formulae for a projectile moving in a vertical plane A 5i A ball is struck by a racket at a point A which is 2m above horizontal ground. Immediately after being struck, the ball has velocity (5i + 8j) ms-1, where i and j are unit vectors horizontally and vertically respectively. 2m B As the ball strikes B, its velocity will have both a horizontal and vertical component The horizontal speed is constant (5) so we do not need to calculate this The vertical speed however will vary as the ball travels so we need to work this out At B the ball has travelled 2m down resolve vertically again, taking downwards as the positive direction After being struck, the ball travels freely under gravity until is strikes the ground at a point B, as shown. Find: a) The greatest height above ground reached by the ball ? = 5.3? ? = 2 ? = 8 ? =? ? = 9.8 ? =? ?2= ?2+ 2?? Sub in values b) The speed of the ball as it reaches B ?2= ( 8)2+2(9.8)(2) Work out right side c) The angle the velocity of the ball makes with the ground as the ball reaches B ?2= 103.2 Square root ? = 10.2?? 1 So as it strikes B, the ball has a velocity of 10.2ms-1 downwards

Kinematics of a particle moving in a straight line or plane (5i + 8j) 8j You can use the constant acceleration formulae for a projectile moving in a vertical plane A 5i A ball is struck by a racket at a point A which is 2m above horizontal ground. Immediately after being struck, the ball has velocity (5i + 8j) ms-1, where i and j are unit vectors horizontally and vertically respectively. 2m B As the ball strikes B, its velocity will have both a horizontal and vertical component The horizontal speed is constant (5) so we do not need to calculate this The vertical speed however will vary as the ball travels so we need to work this out At B the ball has travelled 2m down resolve vertically again, taking downwards as the positive direction After being struck, the ball travels freely under gravity until is strikes the ground at a point B, as shown. Find: a) The greatest height above ground reached by the ball ? = 5.3? 5 You can just use Pythagoras to work out the overall speed! 10.2 b) The speed of the ball as it reaches B = 11?? 1 52+ 10.22 = c) The angle the velocity of the ball makes with the ground as the ball reaches B B = 11?? 1 (2??)

Kinematics of a particle moving in a straight line or plane (5i + 8j) 8j You can use the constant acceleration formulae for a projectile moving in a vertical plane A 5i A ball is struck by a racket at a point A which is 2m above horizontal ground. Immediately after being struck, the ball has velocity (5i + 8j) ms-1, where i and j are unit vectors horizontally and vertically respectively. 2m B We can use the same diagram to calculate the angle between the velocity and the ground After being struck, the ball travels freely under gravity until is strikes the ground at a point B, as shown. Find: 5 ???? =??? ??? Sub in values a) The greatest height above ground reached by the ball ? = 5.3? 10.2 26.2 5 ???? = 10.2 63.8 Calculate B b) The speed of the ball as it reaches B = 11?? 1 ???? = 0.49 Inverse Tan ? = 26.2 c) The angle the velocity of the ball makes with the ground as the ball reaches B = 63.8 Remember to work out the actual angle between the velocity and (Subtract from 90 ) ? = 63.8

Kinematics of a particle moving in a straight line or plane You can use calculus for a particle moving in a straight line, with acceleration that varies with time Displacement (x) Differentiate Integrate The SUVAT equations can be used when acceleration is constant and a particle is moving in a straight line. Velocity (v) Differentiate Integrate If the acceleration of a particle varies, you need to use Calculus Acceleration (a) Velocity is the rate of change of displacement with respect to time Acceleration is the rate of change of velocity with respect to time Therefore, differentiating displacement gives velocity Therefore, differentiating velocity gives acceleration In reverse, use integration! 1B

Kinematics of a particle moving in a straight line or plane You can use calculus for a particle moving in a straight line, with acceleration that varies with time ? = ?4 32? + 12 Differentiate x with respect to t ?? ??= 4?3 32 Displacement (x) dx/dt is the velocity Differentiate Integrate ? = 4?3 32 Velocity (v) Differentiate Integrate Acceleration (a) ? = 4?3 32 A particle P is moving along the x-axis. At time t seconds, the displacement x metres from O is given by: Sub in t = 3 ? = 4(3)3 32 Calculate ? = ?4 32? + 12 ? = 76?? 1 Find: The speed of P when t = 3 The value of t for which P is instantaneously at rest The magnitude of acceleration when t = 1.5 a) b) c) 1B

Kinematics of a particle moving in a straight line or plane ? = ?4 32? + 12 You can use calculus for a particle moving in a straight line, with acceleration that varies with time ? = 4?3 32 Displacement (x) If P is instantaneously at rest, it is the time when the velocity is 0 Differentiate Integrate Velocity (v) Differentiate Integrate ? = 4?3 32 Acceleration (a) v = 0 0 = 4?3 32 Add 32 A particle P is moving along the x-axis. At time t seconds, the displacement x metres from O is given by: 32 = 4?3 Divide by 4 8 = ?3 ? = ?4 32? + 12 Cube root 2 = ? Find: a) The speed of P when t = 3 76ms-1 b) The value of t for which P is instantaneously at rest The magnitude of acceleration when t = 1.5 c) 1B

Kinematics of a particle moving in a straight line or plane ? = ?4 32? + 12 You can use calculus for a particle moving in a straight line, with acceleration that varies with time ? = 4?3 32 Differentiate the velocity again to get the acceleration, in terms of t Displacement (x) Differentiate Integrate Velocity (v) ? = 4?3 32 Differentiate Integrate Differentiate v with respect to t Acceleration (a) ?? ??= 12?2 dv/dt is just acceleration A particle P is moving along the x-axis. At time t seconds, the displacement x metres from O is given by: ? = 12?2 ? = ?4 32? + 12 Find: ? = 12?2 Sub in t = 1.5 a) The speed of P when t = 3 76ms-1 b) The value of t for which P is instantaneously at rest 2 seconds The magnitude of acceleration when t = 1.5 ? = 12(1.5)2 Calculate ? = 27?? 2 c) 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) You can use calculus for a particle moving in a straight line, with acceleration that varies with time ? = 6? ?2 Differentiate the velocity to find acceleration ?? ??= 6 2? dv/dt = a A particle is moving along the x-axis. At time t = 0, the particle is at the point where x = 5. The velocity of the particle at time t seconds (where t 0) is (6t t2)ms-1. Find: ? = 6 2? ? = 6 2? ? = 6 2? Sub in t = 2 Sub in t = 4 a) The acceleration of the particle when t = 2 and t = 4 ? = 2?? 2? = 2?? 2 ? = 6 2(2) ? = 6 2(4) Calculate Calculate ? = 2?? 2 ? = 2?? 2 b) An expression for the displacement of the particle from O at time t seconds At t = 2, the acceleration is 2ms-2 in the direction of x- increasing At t = 4, the acceleration is 2ms-2 in the direction of x- decreasing c) The distance of the particle from its starting point when t = 6 Remember to consider the direction of the acceleration! 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) ? = 6? ?2 You can use calculus for a particle moving in a straight line, with acceleration that varies with time Integrate v (remember to include C!) ? =6?2 ?3 3+ ? 2 Simplify terms if possible A particle is moving along the x-axis. At time t = 0, the particle is at the point where x = 5. The velocity of the particle at time t seconds (where t 0) is (6t t2)ms-1. Find: ? = 3?2 ?3 3+ ? The integral of v is x (displacement) ? = 3?2 ?3 3+ ? We need to find C In the question, we were told at time t = 0, the displacement was 5 ? = 3?2 ?3 a) The acceleration of the particle when t = 2 and t = 4 ? = 2?? 2? = 2?? 2 3+ ? b) An expression for the displacement of the particle from O at time t seconds Sub in values 5 = 3(0)2 (0)3 ? = 3?2 ?3 + ? 3 3+ 5 Calculate C c) The distance of the particle from its starting point when t = 6 5 = ? Now we can write the formula for displacement with C = 5 in it ? = 3?2 ?3 3+ 5 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) ? = 3?2 ?3 You can use calculus for a particle moving in a straight line, with acceleration that varies with time 3+ 5 Sub in t = 6 ? = 3(6)2 (6)3 + 5 3 A particle is moving along the x-axis. At time t = 0, the particle is at the point where x = 5. The velocity of the particle at time t seconds (where t 0) is (6t t2)ms-1. Find: Calculate x ? = 41? Remember to read the question! a) The acceleration of the particle when t = 2 and t = 4 ? = 2?? 2? = 2?? 2 We need the particle s displacement from its starting point. As its starting point was 5m from O, it has moved 36m (to get to 41m) b) An expression for the displacement of the particle from O at time t seconds ? = 3?2 ?3 3+ 5 c) The distance of the particle from its starting point when t = 6 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) ? = 2 2? You can use calculus for a particle moving in a straight line, with acceleration that varies with time Integrate ? = 2? 2?2 + ? The integral of a is v, simplify the fraction 2 A particle P is moving along a straight line. At time t = 0, the particle is at a point A and is moving with velocity 8ms-1 towards a point B on the line, where AB = 30m. At time t seconds, where t 0, the acceleration of P is (2 2t)ms-2 in the direction AB. ? = 2? ?2+ ? We know at time t = 0, the velocity is 8 Use these to find the value of C ? = 2? ?2+ ? Sub in values a) Find an expression, in terms of t, for the displacement of P from A at time t seconds 8 = 2(0) (0)2+? Calculate C ? = 8 b) Show that P does not reach B We can now put the value C = 8 into our equation for velocity ? = 2? ?2+ 8 c) Find the value of t when P returns to A d) Find the total distance travelled by P in the interval between the two instances when it passes through A 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) ? = 2? ?2+ 8 ? = 2 2? You can use calculus for a particle moving in a straight line, with acceleration that varies with time ? = 2? ?2+ 8 Integrate v now to get a formula for the displacement x The integral of v is x, simplify the fraction A particle P is moving along a straight line. At time t = 0, the particle is at a point A and is moving with velocity 8ms-1 towards a point B on the line, where AB = 30m. At time t seconds, where t 0, the acceleration of P is (2 2t)ms-2 in the direction AB. ? =2?2 ?3 3+ 8? + ? 2 ? = ?2 ?3 3+ 8? + ? At time t = 0, the particle is a point A We can take A as the starting displacement ie) 0 a) Find an expression, in terms of t, for the displacement of P from A at time t seconds ? = ?2 ?3 3+ 8? + ? 03 3 b) Show that P does not reach B Sub in t = 0, x = 0 c) Find the value of t when P returns to A 0 = (0)2 + 8(0)+ ? Calculate D ? = 0 d) Find the total distance travelled by P in the interval between the two instances when it passes through A So we do not need to include a constant in our formula for x ? = ?2 ?3 3+ 8? 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) ? = ?2 ?3 ? = 2? ?2+ 8 3+ 8? ? = 2 2? Show that P does not reach B Calculate the furthest distance P gets from A This will occur at the time where the velocity is instantaneously 0 You can use calculus for a particle moving in a straight line, with acceleration that varies with time A particle P is moving along a straight line. At time t = 0, the particle is at a point A and is moving with velocity 8ms-1 towards a point B on the line, where AB = 30m. At time t seconds, where t 0, the acceleration of P is (2 2t)ms-2 in the direction AB. ? = 2? ?2+ 8 Set v = 0 and start solving for t Rearrange to an easier quadratic form 0 = 2? ?2+ 8 ?2 2? 8 = 0 Factorise a) Find an expression, in terms of t, for the displacement of P from A at time t seconds ? 4 ? + 2 = 0 2 values for t ? = ?2 ?3 ? = 4 ?? 2 3+ 8? Only the positive value is possible b) Show that P does not reach B ? = 4 c) Find the value of t when P returns to A Now calculate the displacement at time t = 2 ? = ?2 ?3 3+ 8? 23 3 As the maximum distance is 262/3m, and AB is 30m, P will never reach B d) Find the total distance travelled by P in the interval between the two instances when it passes through A Sub in t = 2 ? = (2)2 + 8(2) Work out the displacement 1B 23? ? = 26

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) ? = ?2 ?3 You can use calculus for a particle moving in a straight line, with acceleration that varies with time ? = 2? ?2+ 8 3+ 8? ? = 2 2? Find the value of t when P returns to A This means the displacement from A will be 0 A particle P is moving along a straight line. At time t = 0, the particle is at a point A and is moving with velocity 8ms-1 towards a point B on the line, where AB = 30m. At time t seconds, where t 0, the acceleration of P is (2 2t)ms-2 in the direction AB. ? = ?2 ?3 3+ 8? Sub in x = 0 Multiply by 3 to remove the fraction 0 = 3?2 ?3+ 24? Rearrange to have t3 as positive Factorise Either inside the bracket or outside it must be 0 0 = ?3 3?2 24? 0 = ?(?2 3? 24) a) Find an expression, in terms of t, for the displacement of P from A at time t seconds ?2 3? 24 = 0 ? = 0 ? = 1 ? = 3 ? = 24 ? = ?2 ?3 3+ 8? This is because the particle starts at A Use the Quadratic formula to solve this part ? = ? ?2 4?? b) Show that P does not reach B Max displacement = 262/3 2? Sub in values c) Find the value of t when P returns to A ( 3)2 (4 1 24) 2(1) ? =3 Calculate d) Find the total distance travelled by P in the interval between the two instances when it passes through A ? = 6.62 ?? ? = 3.62 So the particle returns to A 6.62 seconds after leaving it! 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) ? = ?2 ?3 You can use calculus for a particle moving in a straight line, with acceleration that varies with time ? = 2? ?2+ 8 3+ 8? ? = 2 2? The particle starts at A, moves 262/3m away and then comes back A particle P is moving along a straight line. At time t = 0, the particle is at a point A and is moving with velocity 8ms-1 towards a point B on the line, where AB = 30m. At time t seconds, where t 0, the acceleration of P is (2 2t)ms-2 in the direction AB. The total distance travelled in this time is therefore just given by: 2 x 262/3 = 531/3m a) Find an expression, in terms of t, for the displacement of P from A at time t seconds ? = ?2 ?3 3+ 8? b) Show that P does not reach B Max displacement = 262/3 c) Find the value of t when P returns to A 6.62 seconds d) Find the total distance travelled by P in the interval between the two instances when it passes through A 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) You can use calculus for a particle moving in a straight line, with acceleration that varies with time ? = 3???2? Differentiating Sin gives Cos Remember to multiply by 2 (The differential of 2t) Differentiating Cos gives Sin Remember to multiply by 2 (The differential of 2t) ? = 6???2? A small metal ball, moving in a magnetic field, is modelled as a particle P of mass 0.2kg, moving in a straight line under the action of a single variable force F Newtons. At time t seconds, the displacement, x metres, of the ball (B) from A is given by: ? = 12???2? ? = 12???2? Sub in t = /6 6 ? = 12???2 Calculate a ? = 6 3?? 2 ? = 3???2? Find the magnitude of F when t = /6 ? = ?? Sub in m and a ? = (0.2)( 6 3) You know that F = ma, so we need to find the acceleration of the Ball, in terms of t Calculate in surd form Write as a decimal if you need to! ? = 1.2 3 ? ? = 2.08? 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) You can use calculus for a particle moving in a straight line, with acceleration that varies with time A particle P moves on the x-axis. At time t seconds, the velocity of P is vms-1 in the direction of x-increasing, where v is given by. This function shows that the relationships between x, v and a vary depending on time 5?, ? +4 0 ? < 1 You need to consider each time interval carefully ?2, 1 ? 3 ? = 3 49, ? > 3 When t = 0, P is at the origin O. a) Find the lowest speed of P in the interval 1 t 3 b) Sketch a velocity-time graph to illustrate the motion of P in the interval 0 t 6 c) Find the distance of P from O when t = 6 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) The velocity will be at a minimum or maximum when the acceleration is 0. Meaning the particle has either been accelerating and the acceleration is about to act in the opposite direction (maximum) Or, the particle has been decelerating, and the acceleration is increasing, about to cause the particle s velocity to increase again (minimum) Either way, the acceleration at these is instantaneously at 0 Differentiate the velocity in the required time interval, and set it equal to 0 You can use calculus for a particle moving in a straight line, with acceleration that varies with time A particle P moves on the x-axis. At time t seconds, the velocity of P is vms-1 in the direction of x-increasing, where v is given by. 5?, ? +4 0 ? < 1 ?2, 1 ? 3 ? = Write in a differentiatable form 3 49, ? > 3 ? = ? +4 ? = ? + 4? 2 ?2 Differentiate When t = 0, P is at the origin O. ? = 1 + 2 4? 3 Rewrite ? = 1 + 8 a) Find the lowest speed of P in the interval 1 t 3 ?3 Set a = 0 0 = 1 + 8 b) Sketch a velocity-time graph to illustrate the motion of P in the interval 0 t 6 ?3 Rearrange ?3= 8 Calculate t ? = 2 c) Find the distance of P from O when t = 6 So the velocity will be at a maximum at t = 2 (sometimes you will need to check this!) 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) Sub t = 2 into the relevant equation for velocity You can use calculus for a particle moving in a straight line, with acceleration that varies with time ? = ? +4 ?2 Sub in t = 2 A particle P moves on the x-axis. At time t seconds, the velocity of P is vms-1 in the direction of x-increasing, where v is given by. 4 ? = 2 + (2)2 Calculate ? = 3?? 1 5?, ? +4 0 ? < 1 ?2, 1 ? 3 ? = As this was the only value it must be the answer with more than 1 answer you could sub both in and check which gives the biggest/smallest velocity 3 49, ? > 3 When t = 0, P is at the origin O. a) Find the lowest speed of P in the interval 1 t 3 ? = 2 ? = 3?? 1 b) Sketch a velocity-time graph to illustrate the motion of P in the interval 0 t 6 c) Find the distance of P from O when t = 6 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) Sketching a velocity-time graph Consider each section separately You can use calculus for a particle moving in a straight line, with acceleration that varies with time v (ms-1) 5 A particle P moves on the x-axis. At time t seconds, the velocity of P is vms-1 in the direction of x-increasing, where v is given by. 4 3 5?, ? +4 0 ? < 1 2 ?2, 1 ? 3 ? = 1 3 49, ? > 3 0 0 1 2 3 4 5 6 When t = 0, P is at the origin O. t (seconds) For the first second, the velocity increases with time in a linear way, reaching 5ms-1 after 1 second a) Find the lowest speed of P in the interval 1 t 3 ? = 2 ? = 3?? 1 After t = 3, the velocity is constant at 34/9ms-1 b) Sketch a velocity-time graph to illustrate the motion of P in the interval 0 t 6 In the middle section, the velocity varies more, but we know from section a) that the velocity is at a minimum of 3ms-1 at t = 2 We can therefore draw a minimum through this point c) Find the distance of P from O when t = 6 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) Calculating the distance at time t = 6 You will have to work out where the particle is after each section in order to find the overall distance You can use calculus for a particle moving in a straight line, with acceleration that varies with time A particle P moves on the x-axis. At time t seconds, the velocity of P is vms-1 in the direction of x-increasing, where v is given by. ? = 5? Integrate the expression to get the displacement, remember to include C ? =5?2 + ? 2 5?, ? +4 0 ? < 1 We are told at t = 0, P is at the origin (ie, x = 0) (0) =5(0)2 ?2, 1 ? 3 ? = + ? 2 Calculate C 3 49, ? > 3 ? = 0 When t = 0, P is at the origin O. ? =5?2 a) Find the lowest speed of P in the interval 1 t 3 ? = 2 ? = 3?? 1 2 Using our formula for displacement, sub in t = 1 to find where the particle ends this section ? =5(1)2 b) Sketch a velocity-time graph to illustrate the motion of P in the interval 0 t 6 2 Calculate ? = 2.5? c) Find the distance of P from O when t = 6 So after 1 second, the particle is 2.5m away from O 1B

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) So after 1 second, the particle is 2.5m from O Now calculate the distance travelled in the next section You can use calculus for a particle moving in a straight line, with acceleration that varies with time ? = ? +4 Rewrite in an integratable form ?2 A particle P moves on the x-axis. At time t seconds, the velocity of P is vms-1 in the direction of x-increasing, where v is given by. ? = ? + 4? 2 Integrate, including a constant ? =?2 2+4? 1 5?, ? +4 0 ? < 1 1+ ? Rewrite for substitution ?2, 1 ? 3 ? = ? =?2 2 4 3 49, ?+ ? ? > 3 We know that after 1 second, the displacement is 2.5m Sub these in to find D 2.5 =(1)2 4 When t = 0, P is at the origin O. (1)+ ? 2 Calculate D a) Find the lowest speed of P in the interval 1 t 3 ? = 2 ? = 3?? 1 ? = 6 ? =?2 2 4 b) Sketch a velocity-time graph to illustrate the motion of P in the interval 0 t 6 ?+ 6 Now we know D, sub in t = 3 to find the displacement of P at the end of this section ? =(3)2 4 (3)+ 6 2 c) Find the distance of P from O when t = 6 Calculate 1B 16? ? = 9

Kinematics of a particle moving in a straight line or plane Displacement (x) Velocity (v) Acceleration (a) So after 3 seconds, the particle is 91/6m from O Now calculate the distance travelled in the last section You can use calculus for a particle moving in a straight line, with acceleration that varies with time A particle P moves on the x-axis. At time t seconds, the velocity of P is vms-1 in the direction of x-increasing, where v is given by. This is easier! As the velocity is constant, we can just use Distance = Speed x Time to find how far the particle travels from 3 to 6 seconds 5?, ? +4 0 ? < 1 ?2, 1 ? 3 ? = ???????? = ????? ???? 3 49, ? > 3 49 3 ???????? = 3 When t = 0, P is at the origin O. 13? a) Find the lowest speed of P in the interval 1 t 3 ? = 2 ? = 3?? 1 ???????? = 10 So add this to the current displacement to get the final displacement b) Sketch a velocity-time graph to illustrate the motion of P in the interval 0 t 6 9 16+ 10 13= 19 12? c) Find the distance of P from O when t = 6 1B

Kinematics of a particle moving in a straight line or plane You can use calculus with vectors for a particle moving in a plane (up to now was just along a straight line!) Position Vector (r) Differentiate Integrate When a particle is moving in a plane you can describe its position (r), its velocity (v) and its acceleration (a) using vectors. Velocity Vector (v) Differentiate Integrate The relationships between these in two dimensions are the same as they are in one dimension Acceleration Vector (a) Sometimes dot notation is used. A single dot means differentiate once and two dots means differentiate twice. ? = ?? + ?? Dot notation used for a single differentiation ? = ? = ?? + ?? When you integrate using vectors, the constant of integration (C) will also be a vector Dot notation used for a double differentiation ? = ? = ?? + ?? 1C

Position Vector (r) Velocity Vector (v) Acceleration Vector (a) Kinematics of a particle moving in a straight line or plane ? = 3?? +1 You can use calculus with vectors for a particle moving in a plane (up to now was just along a straight line!) 2?2? Integrate each term, remember to include C ? =3?2 ? +1 6?3? + ? 2 At t = 0, the position vector r = (2i 3j) A particle P is moving in a plane. At time t seconds, its velocity, vms-1, is given by: (2? 3?) =3(0)2 ? +1 6(0)3? + ? Calculate C (you might need to group i and j terms and rearrange!) 2 ? = 3?? +1 (2? 3?) = ? 2?2? ? =3?2 When t = 0, the position vector of P with respect to a fixed origin O is (2i 3j)m. Find: ? +1 6?3? + 2? 3? 2 Putting the i and j terms together Factorising the i and j terms separately ? =3?2 ? + 2? +1 6?3? 3? a) The position vector of P at time t seconds 2 3?2 2 1 6?3 3 ? ? = + 2 ? + b) The acceleration of P when t = 3 1C

Position Vector (r) Velocity Vector (v) Acceleration Vector (a) Kinematics of a particle moving in a straight line or plane 3?2 2 1 6?3 3 ? ? = 3?? +1 You can use calculus with vectors for a particle moving in a plane (up to now was just along a straight line!) 2?2? ? = + 2 ? + ? = 3?? +1 2?2? A particle P is moving in a plane. At time t seconds, its velocity, vms-1, is given by: Differentiate to find a ? = 3? + ?? Sub in t = 3 ? = 3?? +1 2?2? ? = 3? + 3? When t = 0, the position vector of P with respect to a fixed origin O is (2i 3j)m. Find: At time t = 3, the acceleration of the particle is (3i + 3j)ms-2 a) The position vector of P at time t seconds 3?2 2 1 6?3 3 ? ? = + 2 ? + b) The acceleration of P when t = 3 1C

Position Vector (r) Velocity Vector (v) Acceleration Vector (a) Kinematics of a particle moving in a straight line or plane You can use calculus with vectors for a particle moving in a plane (up to now was just along a straight line!) ? = 4? 2?? Integrate to get v, include C At t = 3, we know the velocity is 6i ? = 4?? ?2? + ? A particle P is moving in a plane so that, at time t seconds, its acceleration is: 6? = 4(3)? (3)2? + ? Calculate terms ? = 4? 2?? ?? 2 6? = 12? 9? + ? Rearrange to get the missing vector C At t = 3, the velocity of P is 6ims-1 and the position vector of P is (20i + 3j)m with respect to a fixed origin O. Find: 6? + 9? = ? a) The angle between the direction of motion of P, and i, when t = 2 ? = 4?? ?2? 6? + 9? Group i and j terms and factorise Sub in t = 2 to find the velocity vector Calculate terms ? = 4? 6 ? + ( ?2+ 9)? b) The distance of P from O when t = 0 ? = 4(2) 6 ? + ( (2)2+9)? ? = 2? + 5? 1C