Kinetic Molecular Theory of Gases

Kinetic Theory of Gases UNDERSTANDING THE KINETIC MOLECULAR THEORY AS IT PERTAINS TO GASES

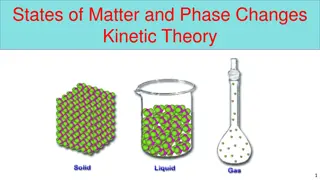
Important Gas Characteristics Gases are highly compressible External forces compress gas samples and decrease volume, removal of external force allows volume to increase Gases are thermally expandable Volume increases as gas temperature increases, and decreases when cooled Gases have high viscosity Gases have a very low resistance to flow and therefore very little internal friction Most gases have low densities Gas densities tend to be 1000 times lower than liquids and solids Gases are infinitely miscible (mixable) Gases mix in any proportion air is a mixture of many gases

Understanding Gases Understanding gases requires an understanding of gas behavior, this can be approached from two perspectives 1. Mathematical interpretation Mathematical analysis of gases results in a set of Gas Laws based on an Ideal Gas 2. Conceptual description Kinetic Molecular Theory used to describe observations that lead to Ideal Gas Laws

Kinetic Molecular Theory Describes characteristics of an imaginary Ideal Gas All real gases require their own set of descriptive characteristics, not feasible due to large number of known gases Creation of imaginary gas that approximates the behavior of all real gases Kinetic Molecular Theory description of ideal gas so closely describes ideal gas that any errors can be overlooked There are three fundamental assumptions

Assumption #1 Gas is composed of particles usually molecules or atoms Small, hard spheres Insignificant volume; relatively far apart from each other No attraction or repulsion between particles

Assumption #2 Particles in a gas move rapidly in constant random motion Moving in straight paths, changing direction only when colliding with one another or other objects Average speed of O2in air at 20 oC is 1660 km/h or 1030 MPH

Assumption #3 Collisions are perfectly elastic Kinetic energy is transferred without loss from one particle to another Total kinetic energy remains constant (conserved)

Mathematical Variables There are four commonly accepted gas law variables 1. Temperature 2. Pressure 3. Volume 4. Amount (moles)

Gas Temperature All temperature values used for describing gases are in terms of absolute kinetic energy content of the system Temperature values must be converted to the Kelvin Scale Kelvin = Celsius + 273 Temperature of a gas is the average kinetic energy of all the particles within they container

Gas Pressure Defined as the force exerted by a gas per unit surface area of its container Due to force and number of collisions Atmospheric pressure 101.325kPa = 1 atm = 760 mm Hg = 14.7 PSI (lb/in2) Barometer is used to measure atmospheric pressure; dependent upon weather Atmospheric pressure (atm) is the weight of a column of air above a unit area No particles present no collisions possible - vacuum

Temperature Pressure Relationship As container of gas is heated, average kinetic energy increases Increase in average kinetic energy leads to greater force acting on the surface area of container Temperature increase = Pressure increase

Gas Volume Volume is a measure of the amount of room available for the gas particles to move around Available room for particles to move around is equal to the volume of the container holding the gas Decreasing size of container results in increasing pressure of contained gas, increasing container size decreases gas pressure. As container size decreases, average number of collisions increases Increase in number of collisions leads to greater force acting on the surface area of container Volume decrease = Pressure increase

Amount of Gas (Moles) Amount of gas is always expressed in moles and represented by the symbol (n) Experience has shown that the number of objects in a system is more descriptive than the mass of the objects. Each gas s unique mass would create major difficulties when working with gas law mathematics Fundamental gas law concept states that all gases can be approximated as being the same, therefore gases of same number of particles will act similarly

Conclusions 1. When temperature is held constant, the density of a gas is proportional to pressure, and volume is inversely proportional to pressure. 2. If volume is kept constant, the pressure of a given number of gas particles is proportional to temperature 3. Holding pressure constant, causes the temperature of a gas to be proportional to volume, and inversely proportional to density

Boyles Law If temperature is constant As the pressure of a gas increases, the volume decreases For a given amount of gas at constant temperature, the volume of a gas varies inversely to pressure As volume increases, pressure decreases As volume decreases, pressure increases ?1?1= ?2?2

Sample Problem #1 If 4.41??3 of nitrogen gas are collected at a pressure of 94.2???, what will the volume be for this gas at 1 atm if the temperature does not change? 1??? = 101.325??? ?1?1= ?2?2 = ?2=94.2??? 4.41??3 ?1?1 ?2 = 4.1??3 101.325???

Charles Law As the temperature of an enclosed gas increases, the volume increases, if the pressure is constant. Volume of a fixed amount of gas is directly proportional to its Kelvin temperature, if pressure remains constant As volume goes up/down, temperature goes up/down ?1 ?1=?2 ?2

Sample Problem #2 With a constant pressure, the volume of a gas is increased from 15.0 liters to 32.0 liters. If the new temperature is 20.0 oC, what was the original temperature? Temperature must be in Kelvin ?????? = ??????? + 273 = 20 + 273 = 293 ?1 ?1=?2 ?1 ?2 ?2 ?2= ?1= 15.0? 293? 32.0?= 137?

Gay-Lussacs Law As the temperature of an enclosed gas increases, the pressure increases, if the volume is constant The pressure of a gas is directly proportional to the Kelvin temperature if the volume remains the constant ?1 ?1=?2 ?2

Sample Problem #3 The pressure in a tire is 1.8 atm at 20 oC. After a 200 mile trip, the pressure reading for the tire is 1.9 atm. What is the temperature inside the tire at the new pressure? Temperature must be in Kelvin ?????? = ??????? + 273 = 20 + 273 = 293 ?1 ?1=?2 ?2 ?1 ?2 293? 1.8???= 309? ?1= ?2= 1.9???