KMP Algorithm Table Computation and String Matching Modification
Learn how to compute the next table using the KMP algorithm for a given string and modify the KMP string matching algorithm to find the largest prefix of a substring match. Additionally, compute the minimal cost matrix to change one string to another character by character.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Homework #7 Rick Lee
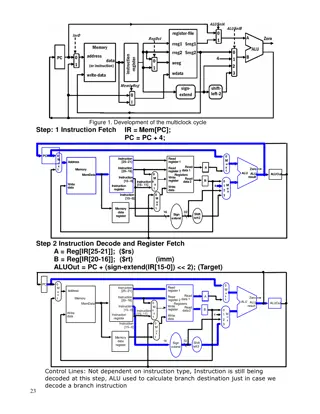
Problem 1 Compute the next table as in the KMP algorithm for the string babbabbbb . Show the details of your calculation i 1 B -1 2 a 0 3 b 0 4 b 1 5 a 1 6 b 2 7 b 3 8 b 4 9 b 1 B next
Problem 1(Cont.) i 1 b -1 2 a 0 3 b 0 4 b 1 5 a 6 b 7 b 8 b 9 b B next Initial: ????[1] = 1, ????[2] = 0 When ? = 3, ? = ????[? 1] + 1 = 1, Because ?[? 1] ?[1], ? = ????[1] + 1 = 1 + 1 = 0 ???? 3 = 0 When ? = 4, ? = ????[? 1] + 1 = 1, Because ? ? 1 = ?[1] ???? 4 = 1
Problem 1(Cont.) i 1 b -1 2 a 0 3 b 0 4 b 1 5 a 1 6 b 2 7 b 3 8 b 9 b B next When ? = 5,? = ????[? 1] + 1 = 2, Because ?[? 1] ?[2], ? = ???? 2 + 1 = 0 + 1 = 1 Because ? ? 1 = ? 1 ????[5] = 1 When ? = 6,? = ????[? 1] + 1 = 2, Because ?[? 1] = ?[2] ???? 6 = 2 When ? = 7,? = ????[? 1] + 1 = 3, Because ? ? 1 = ?[3] ???? 7 = 3
Problem 1(Cont.) i 1 b -1 2 a 0 3 b 0 4 b 1 5 a 1 6 b 2 7 b 3 8 b 4 9 b 1 B next When ? = 8,? = ????[? 1] + 1 = 4, Because ? ? 1 = ?[4] ???? 8 = 4 When ? = 9,? = ????[? 1] + 1 = 5, Because ?[? 1] ?[5],? = ????[5] + 1 = 1 + 1 = 2 Because ?[? 1] ?[2],? = ????[2] + 1 = 0 + 1 = 1 Because ?[? 1] = ?[1] ????[9] = 1
Problem 2 Modify the KMP string matching algorithm to find the largest prefix of B that matches a substring of A. In other words, you do not need to match all of B inside A; instead, you want to find the largest match (but it has to start with ?1).
Problem 3 Given two strings ? = ????? and ? = ??????, compute the minimal cost matrix ?[0..5,0..6] for changing the first string character by character to the second one. Aside from giving the cost matrix, please show the details of how the entry ?[5,6] is computed.
Problem 3(Cont.) b 1 1 1 1 2 3 4 b 2 2 2 1 2 3 3 a 3 3 2 2 1 2 3 a 4 4 3 3 2 1 2 a 5 5 4 4 3 2 2 b 6 6 5 4 4 3 2 0 0 1 2 3 4 5 0 1 2 3 4 5 a b a a b ? 4,6 + 1 ? 5,5 + 1 ? 4,5 ,? 5 = ? 6 ? 5,6 = ??? = min 4,3,2 = 2
Problem 4 Design an algorithm that, given a set of integers ? = ?1,?2, ,??, finds a nonempty subset ? ?, such that ?? 0 ??? ? ?? ? Before presenting your algorithm, please argue why such a nonempty subset must exist.
Problem 4(Cont.) Let ??= ?1,?2, ??, so if 1 ? < ? ?, ?? ??. Let ?? is the sum of ?? mod ?, so its value can be 0,1, ,? 1. If ??= 0, ?? is the required subset. Else, because the value of ?? only can be 1, ,? 1, and we have ? remainders, so according to Pigeonhole principle, there must be two remainder with the same value. So, we can find (?,?) that ??= ??,1 ? < ? ?. The required subset is Sj Si= ??+1 , ,??.
Problem 5 You are asked to design a schedule for a round-robin tennis tournament. There are ? = 2? (? 1) players. Each player must play every other player, and each player must paly one match per round for ? 1 rounds. Denote the players by ?1,?2, ,??. Output the schedule for each player. (Hint: use divide and conquer in the following way. First, divide the players into two equal groups and let them play within the groups for the first ? the games between the groups for the other ? 2 1 rounds. Then, design 2rounds.)
Problem 5(Cont.) 1 2 1 4 3 6 5 8 7 2 3 4 1 2 7 8 5 6 3 4 3 2 1 8 7 6 5 4 5 6 7 8 1 2 3 4 5 6 7 8 5 4 1 2 3 6 7 8 5 6 3 4 1 2 7 8 5 6 7 2 3 4 1 1 2 3 4 5 6 7 8