Limits in Calculus: Concepts and Application

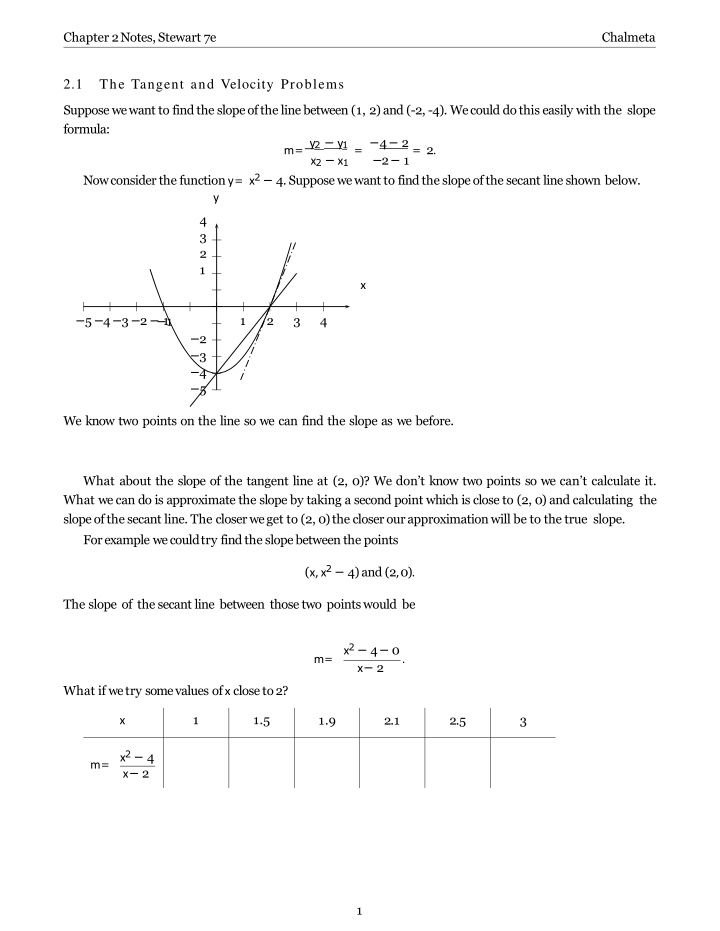
Chapter 2 Notes, Stewart 7e Chalmeta 2.1 The Tangent and Velocity Problems Suppose we want to find the slope of the line between (1, 2) and (-2, -4). We could do this easily with the slope formula: m =y2 y1= 4 2= 2. x2 x1 Now consider the function y = x2 4. Suppose we want to find the slope of the secant line shown below. y 2 1 4 3 2 1 x 5 4 3 2 11 1 2 3 4 2 3 4 5 We know two points on the line so we can find the slope as we before. What about the slope of the tangent line at (2, 0)? We don t know two points so we can t calculate it. What wecan do is approximate the slope by taking a second point which is close to (2, 0) and calculating the slopeofthesecant line.The closerweget to (2,0)thecloserourapproximationwill be to thetrue slope. For example we couldtry find the slope between the points (x, x2 4) and (2,0). The slope of the secant line between those two points would be x2 4 0 x 2 m= . What if we try some values of x close to2? 1 1.5 1.9 2.1 2.5 3 x x2 4 x 2 m= 1

Chapter 2 Notes, Stewart 7e Chalmeta Example 2.1.1. The point P(0.5, 2) lies on the curve y = 1/x. If Q is the point (x, 1/x), use your calculator to find the slop of the secant line PQ for the following values ofx. a).8 b).6 c) .51 d) .49 e) .45 Guess the value of the slope of the tangent line at P(0.5,2). Average Velocity change indistance change intime Average Velocity= Distance is usually given as a function of time s = s(t). This function tells us that if we know how long the object has been moving, t, we know where it is in space s(t). Example 2.1.2. Suppose that the position of anobject moving in a straight line is given by the equation s= t3/6 where t is in seconds, s in meters. Find the average velocity over the given time periods then find the instantaneous velocity whent= 1. 1. [1,3] 2. [1,2] 3. [1,1.5] 4. [1,1.1] 2

Chapter 2 Notes, Stewart 7e Chalmeta 2.2 The Limit of a Function The Question: What happens to f(x) as x approachesa? The Mathematical notation: lim f(x) = L x a In words: The limit of f(x) as x approaches a, equalsL Consider the following functions y y 6 6 h 4 4 2 2 x x 3 2 1 3 2 1 1 2 3 4 1 2 3 4 x2 4 x 2 f(x) = x+ 2 g(x)= f(2) = 4 g(2) isundefined As x gets close to2, As x gets close to2, y = f(x) gets close to 4. y = g(x) gets close to4. lim f(x) = lim g(x) = 4 x 2 x 2 Translation: So when we write lim f(x) = L what we mean in English is As x gets CLOSE to a then f(x) gets CLOSE to L . x a In Words: So when we write lim f(x) = L what we say out loud is The limit as x gets approaches a of f(x) is x a L . The key word here isCLOSE. 3

Chapter 2 Notes, Stewart 7e Chalmeta Consider the following graph: y 4 3 2 1 x 4 3 2 1 1 2 3 4 5 6 7 1 2 3 4 Evaluate thefollowing: (a) lim f(x) = (b) lim f(x) = (c) lim f(x) = x 3 x 1 x 3 (d) f( 3)= (e) f(1) = (f) f(3) = One SidedLimits The limit as x approaches a from the left: lim f(x) = L x a The limit as x approaches a from the right: lim f(x) = L x a+ The limit exists if and only if the limit from the left is equal to the limit from the right. lim f(x) = L lim f(x) = lim f(x) = L x a x a+ x a InfiniteLimits lim f(x) = x a 1 For example f(x) = tan x or f(x) = (x+ 2)2 4

Chapter 2 Notes, Stewart 7e Chalmeta Example 2.2.1. Sketch the graph of the following function and use it to determine the values of a for which lim f(x) exists: x a 2 x if x < 1 if 1 x < 1 f(x) = x if x 1 (x 1)2 4 3 2 1 3 2 1 1 1 2 3 4 2 3 Example 2.2.2. Sketch the graph of a function f that satisfies these conditions: f( 2) = 1. lim f(x) = 4, x 3+ lim f(x) = 2, x 3 lim f(x) = 2, x 2 f(3) = 3, 5

Chapter 2 Notes, Stewart 7e Chalmeta Example 2.2.3. Determine the infinite limits: 6 a) lim x 5+ x 5 6 b) lim x 5 x 5 x 1 c) lim x 0 x2(x+ 2) Example 2.2.4. Determine the limits from the graph of f(x). y 4 3 2 1 x 1 2 3 4 5 1 1 5 4 3 2 2 3 4 5 a) lim f(x) = x 3+ b) lim f(x) = x 3 c) lim f(x) = x 3+ d) lim f(x) = x 3 6

Chapter 2 Notes, Stewart 7e Chalmeta 2.3 Calculating Limits Using the Limit Laws Recall: Notation lim f(x) = L means as x gets close to a, f(x) gets close to L. x a Limits have certain properties which make them easy to work with. Properties: Suppose lim f(x) = L and lim g(x) = K, x a x a then: 1) lim b f(x) = b L x a 2) lim [f(x) g(x)] = L K x a 3) lim [f(x) g(x)] = L K x a f (x) g(x) L K when K = 0 = 4) lim x a 5) lim [f(x)]n = Ln x a We can use these properties to help us solve limits analytically (using algebra). Example 2.3.1. lim x2 + 7x + 2 x 2 EVERY time you get to a limit problem the first thing you always want to do is to plug in the x value that you are given. STEP 1: Always plug in the x value. f(2) = 4 + 14 + 2 = 20 If you get a number, as in this case, then the problem is done. Here the answer is 20. As x gets close to 2, x2 + 7x + 2 gets close to 20 2x2 x 3 x+ 1 Example 2.3.2. lim x 1 2 2( 1) ( 1) 3 0 0 STEP 1: Plug in for x: = ( 1) + 1 0 0 Here we didn t get a number but rather an undefined expression of the form do some algebra and cancel some commonfactors. . This means that we can 7

Chapter 2 Notes, Stewart 7e Chalmeta Step 2: Do some algebra and cancel. 2+ x 2 Example 2.3.3. lim x x 0 2+ 0 2 0 0 STEP 1: Plug in for x: = 0 0 0 Here we didn t get a number but rather an undefined expression of the form do some algebra and cancel some commonfactors. . This means that we can Step 2: Do some algebra and cancel. In this case we can t factor so we will multiply by the conjugate of the numerator to get rid of the square roots. This is known as rationalizing the numerator. 8

Chapter 2 Notes, Stewart 7e Chalmeta 9 t Example 2.3.4. lim x 3 3 t 1 1 Example 2.3.5. lim x+4 4 x 0 x if x < 2 3x+ 9 2 x 1 Example 2.3.6. lim f(x) if f(x) = x 2 if x > 2 9

Chapter 2 Notes, Stewart 7e Chalmeta (x + h)2 x2 h Example 2.3.7. lim h 0 STEP 1: Plug in for h = 0: 0 0 Here we didn t get a number but rather an undefined expression of the form can do some algebra and cancel some common factors. . This means that we Step 2: Do some algebra and cancel. In this case we will multiply out the numerator. f(x+ h) f(x) h 2 where f(x) = x 4x. Example 2.3.8. Find lim h 0 f (x+h) s f (x) s 4x x+ h)2x (x2x f (x+ h) f(x) ) ( 4(x+ h ) lim h 0 = lim h 0 h h 1 0

Chapter 2 Notes, Stewart 7e Chalmeta The Squeeze Theorem If f(x) g(x) h(x) when x is near a (except possibly a)and lim f(x) = lim h(x) = L x a x a then lim g(x) = L x a .1 2 Example 2.3.9. Evaluate lim x sin x 0 x f(x) = x2 y 0.15 0.10 0.05 x 1.0 0.5 0.5 1.0 0.05 0.10 0.15 2 h(x) = x y f(x) = x2 0.05 x 0.2 0.1 0.1 0.2 0.3 2 0.05 h(x) = x 11

Chapter 2 Notes, Stewart 7e Chalmeta 2.4 The Precise Definition of a Limit Recall: A. Informal Definition ofLimit Let f(x) be definedonan open interval about aexcept possibly at aitself. Iff(x) gets arbitrarily close to L (as close to L as we like) for all x sufficiently close to a, we say that f approaches the limit L as x approaches a andwewrite: limf(x) = L ( the limitoff(x), asx approachesa,equalsL ). x a Notes: (1) x a means that you approach x = a from both sides of a. (2) f(a) does not have to bedefined. B. Solving aninequality 1. Fill in the blanks: To say that |x 3| <1 means that x is less than units from . 2. Solve |x 3| <1 Deftnition 2.1. The Deftnition of Limit Let f(x) be defined on an open interval about a except possibly at a itself. Then we say that f approaches the limit L as x approaches a and wewrite: lim f(x) = L x a if for all > 0 there exists a > 0 such that |f(x) L| < whenever 0 < |x a| < . OR if 0 < |x a| < then |f(x) L| < . 12

Chapter 2 Notes, Stewart 7e Chalmeta Example 2.4.1. Consider the function f(x) = 2x + 5. How close to a= 1, must we hold x to be sure that f(x) lies within 1.5 units of f(a) = 3? In terms of the definition f(x) = 2x + 5, a= 1, L = 3 and = 1.5 the distance between x1 and 1 OR the distance between x2 and 1 is the desired value of . y 6 5 L+ 4 3 L 2 L 1 x x1 x2 2 1 1 2 3 4 1 2 We can also use algebra. We want to know when is |f(x) L| < 1.5? We solve theinequality: |f(x) 3| < 1.5 |( 2x + 5) 3| < 1.5 Example 2.4.2. Use the graph of f(x) = 19 x, a = 10, L = 3 and = 1 to determine the value of using the definitionof lim 19 x = 3. To do this we will find a number such that if 0 < |x 10 then | 19 x 3| <1. | < x 10 y 5 L + 4 3 L L 2 1 x a a + 10 20 1 2 13

Chapter 2 Notes, Stewart 7e Chalmeta Ifthe valueof is not specifiedthen yousolvefor intermsof .This usually involvesusingalgebra onthe inequality |f(x) L| < until youcanget it to looklike|x a| <something.At that point something= . Example 2.4.3. Prove that lim 3x + 5 = 8. x 1 Given any > 0 we need to find > 0 such that 0 < |x a| < 0 < |x 1| < = |(3x + 5) 8| < = |3x 3| < = = |x 1| <3 Let s show that = works in the definition. If 0<|x 1| < = 3 |f(x) L| < . = 3 This suggests that we choose = . 3|x 1|< 3 . then 3 |(3x+ 5) 8| = |3x 3| = 3|x 1| <3 = 3 = . Example 2.4.4. The interior of a typical 1-L measuring cup is a right circular cylinder of radius 6cm. How closely must we measure the height, h, in order to measure out 1 L (1000cm3) with an error of no morethan 1% (i.e. 10cm3)?(Use: V= r2h) 14

Chapter 2 Notes, Stewart 7e Chalmeta Example 2.4.5. Use the Graph of f(x) = x2 to find a number such that |x2 4| < 0.5whenever |x 2| < . y 6 5 L+ L L 4 3 2 1 x x1 x2 1.0 0.5 0.5 1.0 1.5 2.0 2.5 3.0 1 15