Linear Functions: Writing and Graphing in Slope-Intercept Form
Explore the fundamentals of linear functions in slope-intercept form through visual aids and practice problems. Learn to calculate slopes, plot points, determine y-intercepts, and graph equations step-by-step. Enhance your understanding of the concepts with detailed examples and explanations. Dive into the world of linear equations and sharpen your skills in writing and interpreting them in a clear, concise manner.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Warm UP Grab your folder and be ready to review your quiz
2-3 Linear Functions: Slope Intercept Form Day 1 Objective: I can write and graph a linear function in slope intercept form
Slope Sketch and describe the slopes of each graph. Horizontal Change (x2, y2) Vertical Change (x1, y1) Negative Slope Positive Slope Vertical Change (rise) Horizontal Change (run) Slope = 0
Find the slope for each set of points. (x1, y1) and (x2, y2): y y 2 1 x x 2 1 4 7 6 1= 3 6 ( 5) 5 ( 4)=11 7 4 1 6= 3 5 6 4 5= 11 (1,7) and (6, 4) 5 5 (-4, -5) and (5, 6) 9 9
Linear Equation: Slope Intercept form b mx y + = m = 2; y-intercept is (0, -3) mx y = = y 2 y-intercept = b Slope = m + x b + 3 2 m = ; y-intercept is (0, 7) mx y = = y 3 3 + + + b 7 2 x
Linear Equation: Slope Intercept form = = + + x y mx 1 b + 6 y Vertical Change 2 Horizontal Change Horizontal Change = = + + x y mx b Vertical Change 3 y 2
Linear Equation: Slope Intercept form 2 3 = x y Graph: 1. Plot y-intercept 2. Use slope to plot 2nd point. 3. Draw line through points. 2 + = x y Graph: Horizontal Change Vertical Change 4 3
Writing in slope intercept form Solve for y! 2? + 6? = 24 9? 3? = 12 6? = 2? + 24 6 6 6 3? = 9? + 12 3 3 3 ? = 1 3? + 4 ? = 3? 4
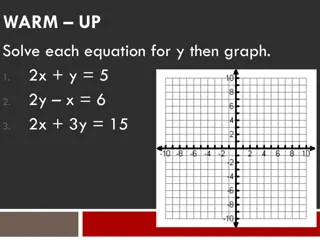
Warm Up What is the slope and y-intercept in the following equations: y = 11x +4 m = 11 y = 4 ? ? Y = y = 2? 2 m = 2 3y + 2 = 6x 3 Find the slope given points: (6,7) and (15,2). 2 7 15 6= ? ?
More Linear Equations Point Slope Form Day 2 Objective: I can write and graph a linear function in point slope form.
Point Slope Form y y m Examples Slope Formula: = 2 1 Point (2, 3) Slope: 4 = y 3 4 x x 2 1 2 ( ) x y y x ( ) 1 x = 1 m x ( ) 1 x x x 2 Point (-3, -7) Slope: = y + 7 3 1 3 Slope m = 2 + 3 ( ) x ( ) y y x x 1 1 Point (-6, 5) Slope: -2 Point (x1, y1) = -2 + 6 ( ) y x 5
Write an equation given two points Equation for the line that passes through (3, 2) and (5, 8) 1. Find the slope. 3 5 Equation for the line that passes through (7, 3) and (3, 11) 3 11 = y OR 11 y 8 2 6 = = = m 3 2 8 = = = m 2. Choose 1 of the given points and substitute into point-slope form. 2 2 = 3 ( ) y x 3 ( 3 7 4 OR = 3 2 7 ) x 8 5 ( ) y x 3 = 2 ( 3 ) x y = 2 = x y = = 2 3 ( 3 3 9 7 ) y x x 8 8 y 3 3 3 = x ( 5 15 7 ) y y x x = 3
Graphing from point-slope form Graph the equation: ) 4 ( 3 ) 3 , 4 ( 3 Graph the equation: + y 2 2 = + = + 3 2 ( 4 ) y x x 5 ) 2 2 , 4 ( 2 Point: Slope: Point: Slope: 5 p.86:10-21, 42- 44, 49 Exit Ticket Today!!!
Warm Up Given the pattern above, make an input output table and write an equation in slope intercept form for the diagram number and the squares per diagram:
More Linear Equations Standard Form Day 3 Objective: I can write and graph a linear function in standard form.
Three Forms of a linear equation y = mx + b b = y-intercept Slope-Intercept Form: m = slope ? =2 3?+5 Point Slope Form: m = slope y y1 = m(x x1) (x1, y1) = point ? 9 =2 3(? 6) Standard Form: where A, B, and C are integers. - meaning no fractions or decimals. Ax + By = C 2? 3? = 15
Slope-Intercept Form to Standard Form Standard Form to Slope-Intercept Form Ax + By = C Add or Subtract mx from both sides. Solve for y! ? = 7 3? + 5? = 15 5? + 3 No fractions or decimals 5? = 3? + 15 7 5? + ? = 3 5( ) ? = 3 5? + 3 7? + 5? = 15 Multiply to eliminate denominators. ? =3 2? + 7 3? + 2? = 14 3? 2? = 14
Graphing a standard form equation Find and graph the intercepts. x-intercept y-intercept ?? + ?? = ? ?? + ?(0) = ? ?(0) + ?? = ? 3x + 5y = 15 15 15 5 y = _________ x = ___________ x = 5 3 ?? + ?? = ? y = 3 ?? = ? ? =? ?? = ? ? =? ? ?
A runner is participating in a 10-kilometer road race and she is currently at the halfway point. She looks at her watch and notices that it has taken her exactly twenty five minutes to get to this point. Assume that she has run at a constant rate and will complete the race at this same rate. Write an equation to represent the distance she has run from where she is now. x = Time (minutes) Slope-intercept Form mx y = y = Distance from 5 km (km) + b 5km Running Rate: 2 . 0 = 25 5 (y-intercept) min 2 . 0 = + 5 y x Starting point:
After a water main break, a large buildings basement was flooded to the ceiling. The local fire department provides two pump trucks to pump the water out. The first truck can pump 25 cubic feet of water per minute and the second truck can pump 32 cubic feet of water per minute. The building is a rectangular prism, measuring 150 feet long, 120 feet wide and 10 feet deep. If both trucks are used for different amounts of time to pump out the basement, write an equation to represent this situation. p. 86:22-31, 36-41 Amount of water 1st Truck +Amount of water 2nd Truck Time spent pumping = Total x = First Truck Standard Form + y = Second Truck 25 x = 32 y 180 000 ,