Linear Regression Models in Machine Learning
Explore the concepts of linear regression models in machine learning, including training methods, model assumptions, and optimization techniques such as Maximum Likelihood Estimation. Understand how linear regression can be used to predict dependent variables based on independent variables, with practical examples and discussions on classifier vs. regression models.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
CSCE-633 Machine Learning 8. Linear regression Instructor: Guni Sharon 0
Announcements Announcements Midterm on Tuesday, April 12 during class Tuesday April 19 , 5 p.m., Last day drop courses with no penalty (Q-drop) Overdue: Due: Programming assignment 2: Linear and Logistic Regression, due by March-15 1
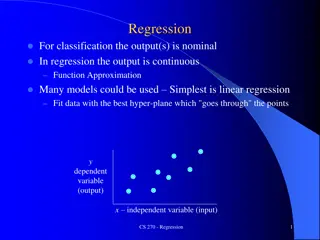
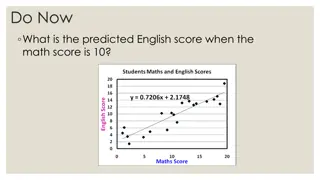
Classifiers vs regression models So far, train a classification model such that ? = most likely ? {?1, ,??} Logistic regression is a classification model assuming continuous (Normally distributed) feature values Today we will discuss a regression model ? = most likely ? where ? E.g., predict height given weight and gender 2
Linear regression Predict a dependent variable, ??, based on the independent variable value ?? Data Assumption: ?? ? Model Assumption: ??= ? ??+ ?? where ?? ?(0,?2) What about the bias term, ?? As we said before, we can simply add it as another dimension in ?, e.g., ? 0 = ?, and in ?,e.g., ? 0 = 1 3
Linear regression ??= ? ??+ ?? where ?? ?(0,?2) Alternatively, we can write: ?? ?(? ??,?2) How do we train ? ? Find ? that best explain the training data ? argmax ? ?? ??|??;? Define ? ??|??;? 2 ?? ? ?? 2?2 1 ? 2?? ? ??|??;? = 4
Optimal ? 2 ?? ? ?? 2?2 1 ? 2?? argmax ? ?? ??|??;? = argmax We previously discussed two approaches Maximum Likelihood Estimation (MLE) Maximum A posteriori Probability (MAP) ? ? 5
Maximum Likelihood Estimation (MLE) 2 2 ?? ? ?? 2?2 ?? ? ?? 2?2 1 1 ? 2?? ? 2?? argmax ? ?ln = argmax ? ? 2 ?? ? ?? 2?2 1 ? 2?+ ln? = argmax ?ln ? Constant w.r.t ? 1 2?2 ??? ? ?? 2= argmin ??? ? ?? 2 = argmin ? ? Constant w.r.t ? 1 ? ?=0 ? ?? ? ?? 2 Let s add a constant factor = argmin Mean Squared Error! ? 6
Ordinary Least Square Linear Regression 1 ? ?=0 ? ?? ? ?? 2 0.5 ? ??2 ? ? = ? = ?1, ,??, ? = ?1, ,?? We can use gradient decent on ?? We can also find the optimal ? in a closed form solution ?? = ? ?? ? = 0 ? ?? ? ? = 0 ? = ? ? 1? ? ? ? ? ? 1 ? ? 1? ?? = ?? ? ? ? 1= ? ? ?? ? ? 1 ? Demo 7
Maximum A posteriori Probability (MAP) Instead of maximizing ? ?;? (MLE), maximize ? ?|? ? ?|? =? ?|? ? ? ? ? ? ?|? : we know how to compute ? that maximizes ? ?|? Same ? that minimizes ? ? = 0.5 ?? ?2 ? ?: we don t care about the normalizing factor (it is not dependent on ?) ? ? : ? is now considered a random variable. We need to assume an underlying distribution ? ?(0,?2) 8
Ridge Regression argmax ? ?|? = argmax ? ?|? ? ? ? ? = argmax ?? ??|??,? ? ? = argmax ln ?? ??|??,? ? ? ? ? = argmax ?ln? ? +ln ?? ??|??;? argmaxln ? ??|??;? ? ? 1 ? ?? ?? 2 = argmax 2?2 ? ? 1 2? ? 2 ?? ?? ?? 2 = argmax 2?? 2?? ? = 0 ? ??2 ?? 1 ? ?[ ? ?? ?? 2? ? +1 ? ?? ?? ?? 2 = argmin ? 2 ? =?? 2] + ? ? 2 = argmin 2 ?? ? 9
Ridge Regression 1 ? ?[ ? ?? ?? ? =?? ?? 2] + ? ? 2 0.5 ?? ?2+ ?? ? ? ? = 2 2 We can find the optimal ? in a closed form solution ?? = ? ?? ? + ??? = ? ?? ? ? + ??? = 0 ? ? + ?? ? ? ? = 0 ? = ? ? + ?? 1? ? Demo 10
What did we learn? Ordinary Least Squares: arg?min0.5 ?? ?2 Squared loss No regularization Closed form: ? = ? ? 1? ? Ridge Regression: arg?min0.5 ?? ?2+ ? ? Squared loss ?2-regularization Closed form: ? = ? ? + ?? 1? ? Why not always use the closed form solution? Matrix inversion is expensive, ?(?3) 2 11
What next? Class: Support Vector Machines Assignments: Programming assignment 2: Linear and Logistic Regression, due by March-15 12