Lines and Rotational Symmetry in 2D Shapes
Learn about lines and rotational symmetry in 2D shapes. Discover how many lines of symmetry different shapes have and the order of rotational symmetry they exhibit. Explore the concepts through explanatory images and explanations on mathssupport.org.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
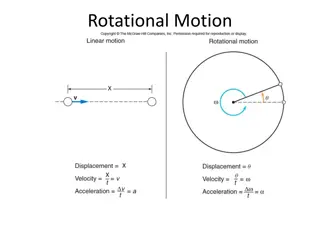
20 March 2025 Line and rotational symmetry LO: To find the number of lines of symmetry a 2D shape has, and the order of rotational symmetry. www.mathssupport.org
Line of symmetry A 2D shape has a line of symmetry when one half of the shape fits exactly over the other half when the shape is folded along that line. A line of symmetry is also called mirror line because the shapes on each side reflect each other. This is called reflected symmetry. Some shapes have no lines of symmetry Tracing paper can be used to check whether a shape has a line of symmetry www.mathssupport.org www.mathssupport.org
Square A square has four lines of symmetry www.mathssupport.org
Rectangle A rectangle has two lines of symmetry. www.mathssupport.org
Parallelogram The parallelogram has no lines of symmetry www.mathssupport.org
Other shapes It has two lines of symmetry It has one line of symmetry It has three lines of symmetry It has four lines of symmetry www.mathssupport.org
Rotational symmetry The order of rotational symmetry that an object has is the number of times that it fits on to itself during a full rotation of 360 degrees. www.mathssupport.org www.mathssupport.org
Parallelogram A parallelogram has rotational symmetry of order ? www.mathssupport.org
Parallelogram A parallelogram has rotational symmetry of order ? 2 2 1 www.mathssupport.org
Rhombus A rhombus has rotational symmetry of order ? www.mathssupport.org
Rhombus 2 A rhombus has rotational symmetry of order ? 2 1 www.mathssupport.org
Rectangle A rectangle has rotational symmetry of order ? www.mathssupport.org
Rectangle 2 A rectangle has rotational symmetry of order ? 2 1 www.mathssupport.org
Square A square has rotational symmetry of order ? www.mathssupport.org
Square A square has rotational symmetry of order ? www.mathssupport.org
Square A square has rotational symmetry of order ? 4 3 4 2 1 www.mathssupport.org
Trapezium A trapezium has rotational symmetry of order ? www.mathssupport.org
Trapezium A trapezium has rotational symmetry of order ? 1 1 www.mathssupport.org
Isosceles trapezium An isosceles trapezium has rotational symmetry of order ? www.mathssupport.org
Isosceles trapezium An isosceles trapezium has rotational symmetry of order ? 1 1 www.mathssupport.org
Kite A kite has rotational symmetry of order ? www.mathssupport.org
Kite 1 A kite has rotational symmetry of order ? 1 www.mathssupport.org
Other shapes www.mathssupport.org
Other shapes Order 1 www.mathssupport.org
Other shapes 1 2 Order 2 Order 1 www.mathssupport.org
Other shapes 1 2 Order 2 Order 1 3 2 1 Order 3 www.mathssupport.org
Other shapes 1 2 Order 2 Order 1 3 3 4 2 1 1 2 Order 4 Order 3 www.mathssupport.org
Thank you for using resources from A close up of a cage Description automatically generated For more resources visit our website https://www.mathssupport.org If you have a special request, drop us an email info@mathssupport.org Get 20% off in your next purchase from our website, just use this code when checkout: MSUPPORT_20 www.mathssupport.org