Logarithmic Functions: Understanding and Application

Warm Up Practice worksheet 3.1 Practice identifying and using the correct formula which is necessary to solve a problem Compound Interests and Annuities

LOGARITHMIC FUNCTIONS AND THEIR GRAPHS C Section 3.2

Objectives Students will be able to Decipher between and use each interest and exponential application formula Determine the difference between a present value and future value annuity Switch between exponential and logarithmic forms (Evaluate logs and natural logs)

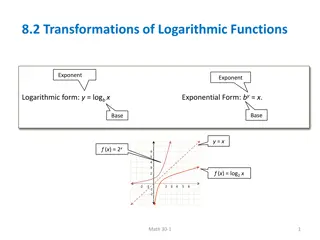
Definition of Logarithmic Function For x > 0, a > 0 and a 1, ? = log?? , if and only if ? = ?? The function given by is called the logarithmic function with base a ? ? = log?? Logarithms are exponents (log?? is the exponent to which a must be raised to obtain x.

Switching Forms 2 = log39 can be re written as 9 = 32 (3 to what power is 9?) 53= 125 can be re written as log5125 = 3

Practice The Meaning of Logarithms Worksheet Problems 1 20 _______ minutes

Closure Exit Ticket On a note card(provided by Miss Young) Write your name! (please) Write the equation in exponential form: log464 = 3 Write the equation in logarithmic form: 9 32= 27 Hand your note card to Miss Young on your way out the door Have a great day!!

Warm Up Write the equation in exponential form: log464 = 3 32= 27 Write the equation in logarithmic form: 9

Objectives Students will be able to Evaluate logs and natural logs Use inverse symmetry to connect exponential and logarithmic graphs Recognize and transform the parent graph of log functions

Evaluating Logarithms 1) ? ? = ???2? , x = 32 2) ? ? = ???3? , x = 1 1 3) ? ? = log4? , x = 2 4) ? ? = log10? , x = 100

Practice: Evaluate the Logarithm 1. y = log216 1 2. y = log2( ) 2 3. y = log416 4. y = log51

Common Logarithmic Function The logarithmic function with base 10 Denoted: log10 This is the log function on your calculator or just log Example: Evaluate the function ? ? = log? at each value of x 1) x = 10 2) x = 1 3 3) x = 2.5 4) x = -2

Properties of Logarithms 1. loga1 = 0 since a0= 1. 2. logaa = 1 since a1= a. 3. logaax= x 4. If logax = logay, then x = y. one-to-one property Examples: 1. Solve for x: log6 6 = x 2. Simplify: log3 35

Properties of Natural Logs (Ln is the exact same idea as logs. Ln is in base e. Logs are (usually) base 10) 1. ln1 = 0 since e0= 1. 2. lne = 1 since e1= e. 3. ln ex= x 4. If ln x = ln y, then x = y. one-to-one property Examples: Simplify e 1 ln 3 ln ln 1 e 2

Graphing Logarithmic Functions The graphs of inverse functions are reflections of each other in the line ? = ? Sketch the graph of ? ? = 2? Sketch the graph of ? ? = log2? ? ? ? = 2?

Graphing Logarithmic Functions Plug in x values that work nicely (Can t use calculator when not base 10) Example: Graph ? ? = log3? (state the changes, VA and x-intercept)

Graphing Logarithmic Functions Logarithmic Function: log?(? ) + ? a shrink or stretch graph (changes shape) h shifts the graph left or right (i.e. (x-2) shifts right 2) k shifts the graph up or down (i.e. x + 2 shifts up 2) Negative log flips graph over x axis

Graphing Logarithmic Functions Example: Graph log3? + 2

Graphing Logarithmic Functions Example: Graph log2(? + 3)

Practice Work on Graphing Logarithms worksheet (finish for homework.

Closure Evaluate: log464 Solve for x: log3x = log3(2x + 1) Graph: log2(? 1) + 4