Magnetic Fields and Currents: Concepts and Problems

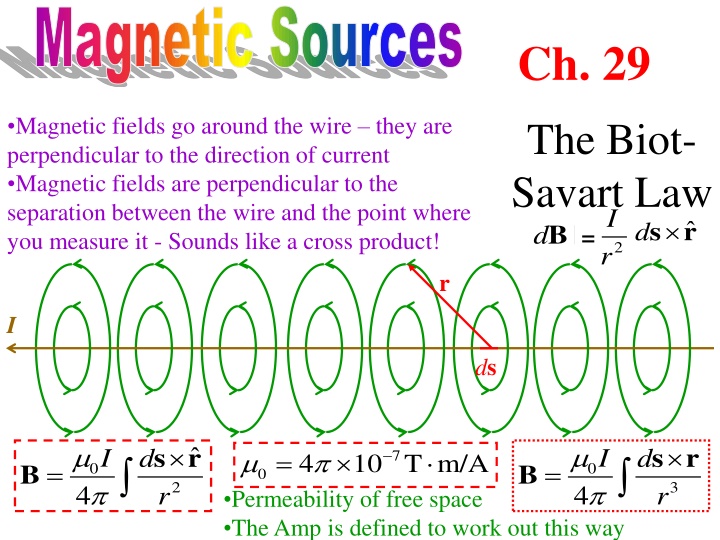
Magnetic Sources Ch. 29 Magnetic fields go around the wire they are perpendicular to the direction of current Magnetic fields are perpendicular to the separation between the wire and the point where you measure it - Sounds like a cross product! The Biot- Savart Law I d r d s r B = 2 r I ds s r s r I I d d = 7 4 10 T m/A = = B B 0 0 0 2 3 4 4 r r Permeability of free space The Amp is defined to work out this way

Quick Quiz 29.1 JIT Consider the magnetic field due to the current in the wire shown in the figure. Rank the points , , and in terms of magnitude of the magnetic field that is due to the current in just the length ele ment shown from greatest to least. A B C ds B >C > A

Sample Problem s r I d = B 0 2 4 r A loop of wire consists of two quarter circles of radii R and 2R, both centered at a point P, and connected with wires going radially from one to the other. If a current I flows in the loop, what is the magnetic field at the point P? ds r ds r I ds r Do one side at a time First do one of the straight segments ds and r-hat are parallel No contribution to the integral Other straight segment is the same Now do inner quarter loop (assume x-y) 4 R Outer loop opposite direction, similar r ds P d = s r 0 R 2R I R k = B 0 k k = s r = d ds 16 I I I 2 ds R k = = 0 R = B k 0 0 inner 8 2 2 4 4 R I R k B 0 outer 16

Magnetic Field from a Finite Wire i j = = d ) ( ( x + + dx i r x a Magnetic field from a finite straight wire: Let a be the distance the point is from the wire Let x be the horizontal separation P Skip Derivation 2 2 r x = a s ( ) i i j + dx x a a I r x = 2 ds B 0 1 2 ) 3 2 4 + x 2 2 a 1 -x1 x I x2 O Ia dx + x x k = 2 0 I a = cos 1 + x + ( ) 3 2 4 1 x 2 2 x a 2 1 2 x a 1 k I x x = cos 2 = + 0 2 + 1 + 2 2 2 2 4 a x a 2 2 2 2 1 2 x a x a Warning: My differs from that of the book ( ) = + cos cos 0 B 1 2 4

Magnetic Field from a Wire I a ( ) = + Magnitude is found from the formula Direction is found from the right hand rule Place thumb in direction of current flow Fingers curl in direction of B-field Infinite wire: Angles are simple 0 cos cos 1 = = cos cos 0 B 1 2 4 a I a 1 2 = 0 B 2 I = = 1 2 1 2 Two wires have the same current I flowing through them. If we want the magnetic field between them to be large and up, we should have the current in the upper one flow _____ and the lower one ______ A) Left , Right B) Left, Left D) Right, Left E) Right, Right

MCAT question Ans D

CT-1-A battery establishes a steady current around the circuit below. A compass needle is placed in the plane of the circuit successively just to the above points P, Q, and R (where the letters are) in the plane of the circuit. The relative deflection of the needle, in de-scending order, is A.P, Q, R. B.Q, R, P. C.R, Q, P. D.P, R, Q. E.Q, P, R Ans E

Sample problem I A regular hexagon whose center is a distance a = 1 cm from the nearest side has current I = 4.00 A flowing around it. The current flows N = 500 times around. What is the total magnetic field at the center? Draw in the two directions from the center to the corners of one segment Top angle is one-sixth of a circle, or 60 degrees Total angles in circle is 180, so other two angles are 60 each Use formula to get magnetic field right hand rule says up. ( ) cos60 cos60 4 a 60 a 60 60 I I a = + = 0 0 B 4 Multiply by all six side, and then by 500 cycles 6 4 a ( )( ) 7 6 4 10 T m/A 4 4 A 500 IN = = = 0 0.120 T B ( ) tot 0.01 m

I Right Hand Rule for Loops If you curl your fingers in the direction the current flows, thumb points in direction of B-field inside the loop Works for solenoids too (later) B Curl fingers around I and Thumb point to Mag dipole moment. Also gives B inside a loop

Warmup 14

Force Between Parallel Wires I1 d F I2 L 0 1 I d = One wire infinite creates a magnetic field Other wire finite or infinite feels the force B 2 = F L B 2I I I 2 F L = 0 1 2 2 d Attractive if current is parallel, repulsive if anti-parallel

JIT Quick Quiz 29.2 Ans A

CT-2 Two parallel wires are connected to two separate DC power supplies so that the direction of their currents are initially parallel. When the leads to one of the wires are reversed I2 I1 + - + - A.The wires move closer to each other B.The wires mover apart C.The wires do not move. Ans B

CT-3- Consider two parallel wires carrying currents I1 and I2 respectively. The wires are a small distance a apart. Which of the following (is) are true: A.If I1 = 2I2 and the directions of the currents are in the same direction, then the attractive force on the wire carrying I2 is 2 times that on the wire carrying I1. B.If I1 = 2I2 and the directions of the currents are in the same direction, then the attractive force on the wire carrying I1 is 2 times that on the wire carrying I2. C.If the magnitudes of the currents are the same but their directions are opposite to each other the magnetic field at a distance r > a is twice what it would be if only one wire were present. D.If the magnitudes of the currents are the same but their directions are opposite to each other the magnetic field at a distance r > a is zero or close to zero. E.Two of the above F.None of the above Ans D

Warmup 14

Amperes Law (original recipe) Suppose we have a wire coming out of the plane Let s integrate the magnetic field around a closed path There s a new symbol for such an integral Circle means over a closed loop The magnetic field is parallel to direction of integration I r What if we pick a different path? I a = 0 B 2 ds = = 2 0 r 0I dscos ? ?? = ? ?? 2 r d ?0? 2?? I = ??? ? ?? = ???cos? = cos ds rd ? ?? = ?0? We have demonstrated this is true no matter what path you take We don t even need a straight infinite wire All that matters is that current passes through the closed Ampere loop

Understanding Amperes Law If multiple currents flow through, add up all that are inside the loop Use right-hand rule to determine if they count as + or Curl fingers in direction of Ampere loop If thumb points in direction of current, plus, otherwise minus The wire can be bent, the loop can be any shape, even non-planar ? ?? = ?0? There are currents going in and out of the screen as sketched at right. What is the ingtegral of the magnetic field around the path sketched in purple? A) 0(11 A) B) 0(-11 A)C) 0(3 A) D) 0(-3 A) E) None of the above 1 A 2 A 4 A 5 A 7 A Right hand rule causes thumb to point down Downward currents count as +, upwards as Note. If point thumb in direction of net current and sum in direction of curled fingers, sum will be positive B points in that direction. ? ?? = ?04 A 2 A 5 A

JIT Quick Quiz 29.3 Rank the magnitudes of d for the closed paths in the figure, from greatest to least. Ans c>a>d>b

JIT Quick Quiz 29.4 Rank the magnitudes of d for the closed paths in the figure, from greatest to least. Ans a=c=d>b

Using Amperes Law Ampere s Law can be used rarely to calculate magnetic fields Need lots of symmetry usually cylindrical A wire of radius a has total current I distribu- ted uniformly across its cross-sectional area. Find the magnetic field everywhere. I I End-on view Draw an Ampere loop outside the wire it contains all the current Magnetic field is parallel to the direction of this loop, and constant around it Use Ampere s Law But we used a loop outside the wire, so we only have it for r > a = 2 rB ?0? = ? ?? = ? ?? I r = 0 B 2

Using Amperes Law (2) Now do it inside the wire Ampere loop inside the wire does not contain all the current The fraction is proportional to the area Ir a = 2 rI I r a = a 2 2 rI 2 = 2 rB ?0??= ? ?? rI r Ir a 2 2 I r a r r a a = = End-on view 0 0 B 0 Ir = B 2 2 2 2 0

Warmup 15

Solenoids Consider a planar loop of wire any shape with a current I going around it Now, stack many, many such loops Treat spacing as very closely spaced Assume stack is tall compared to size of loop Outside, most of the field cancels for ideal solenoid (long, thin, tightly packed) outside neglible (ideal solenoid) B

Field Inside a Solenoid It remains only to calculate the magnetic field inside We use Ampere s law Recall, neglible B-field outside = B L = I NI ?0?tot= ? ?? in tot There may be many (N) current loops within this Ampere loop Let n = N/L be loops per unit length NI B L Works for any shape solenoid, not just cylindrical For finite length solenoids, there are end effects L = B nI = 0 in 0 in

JIT Quick Quiz 29.5 Consider a solenoid that is very long compared with its radius. Of the following choices, what is the most effective way to increase the magnetic field in the interior of the solenoid? (a) double its length, keeping the number of turns per unit length constant (b) reduce its radius by half, keeping the number of turns per unit length constant (c) overwrap the entire solenoid with an additional layer of current-carrying wire Ans C

Magnetic Flux Magnetic flux is defined exactly the same way for magnetism as it was for electricity B n dA B A cylindrical solenoid of radius 10 cm has length 50 cm and has 1000 turns of wire going around it. What is the magnetic field inside it, and the magnetic flux through it, when a current of 2.00 A is passing through the wire? ( ) 1000 2 A 0.5 m = 0.00503 T B = B nI = 7 4 10 T m/A in 0 in ( ) ( ) 2 = = = B R BA 0.00503 T 0.1 m 2 B = 1.579 10 T m 4 2 A Tesla meter2 is also called a Weber (Wb) B

Gausss Law for Magnetism Magnetic field lines always go in circles there are no magnetic monopole sources For closed surfaces, any flux in must go out somewhere else ? ? ??? = 0 A regular tetrahedron (four sides, all congruent) has a cylin- drical magnet placed in the middle of the bottom face. There is a total of 0.012 T m2 of magnetic flux entering the bottom face. What is the total flux from one of the three top faces? A) 0.006 T m2 B) 0.004 T m2 D) 0.012 T m2 E) None of the above C) 0.003 T m2 Flux in bottom must equal total flux out other three sides Other three sides must have equal flux, by symmetry 0.012 T m + + = Sign of entering flux is negative = 2 2 3 0.012 T m 1 2 3 1

CT-4 - A sphere of radius R is placed near a long, straight wire that carries a steady current I. The magnetic field generated by the current is B. The total magnetic flux passing through the sphere is A. oI. B. oI/(4 R 2 ). C. 4 R 2/ o I. D. zero. E. need more information Ans D

Ex A cube of edge length = 2.50 cm is positioned as shown below. A uniform magnetic field given by B = (5.00 i + 4.00 j + 3.00 k) T exists throughout the region. (a) Calculate the flux through the shaded region. (b) What is the total flux through the six faces? Solve on Board

Warmup 15 http://www.youtube.com/watch?v=A1vyB-O5i6E