Markov Chains Seminar: Classical and Useful Insights
Delve into the world of classical and useful Markov chains with topics like Gambler’s Ruin, Coupon Collecting, Hypercubes, and more. Understand the probabilities, expected times, and applications in this informative seminar led by Tomer Haimovich.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Classical (and Useful) Markov Chains Markov Chains Seminar, 9.11.2016 Tomer Haimovich
Outline 1. Gambler s Ruin 2. Coupon Collecting 3. Hypercubes and the Ehrenfest Urn Model 4. Random Walks on Groups 5. Random Walks on
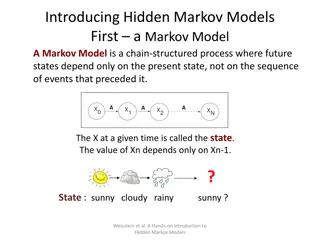
Introduction A gambler bets on the outcomes of independent fair coin tosses If it s heads, she wins 1. if it s tails, she loses 1 If she reaches 0 or ?, she stops gambling When will the gambler reach one of the two outcomes? What are the probabilities of the two possibilities? 0 k n K-1 K+1
Definitions Let ??be gambler s fortune at time ? Let ? be the time to reach one of ? or 0 Assume that ?0= ?, where 0 ? ? ??{??= ?}: the probability of reaching ? after ? steps, when starting in ?0= ? ??? : the expected time to reach one of ? or 0
Probability of Reaching ? Denote by ?? the probability that the gambler ended at ? ?0= 0, ??= 1 For 1 ? ? 1: ??=1 2?? 1+1 2??+1 And when we solve the system of linear equations: ??=? ?
Expected Time to be Absorbed Define ?? ??(?), the expected time to be absorbed, starting at position ? ?0= ??= 0 For 1 ? ? 1: ??=1 21 + ??+1 +1 21 + ?? 1 And when we solve the system of linear equations: ??= ? ? ?
Introduction ? different types of coupons. Gotta catch em all! Each new coupon is equally likely to be each of the ? types How many coupons must be obtained to collect all ? types?
Why is it even a Markov Chain? Let ?? denote the number of different types the collector has, after obtaining ? coupons ?0= 0 ? ?,? + 1 = ? ??+1= ? + 1 | ??= ? =? ? ? ?,? = ? ??+1= ? | ??= ? =? ? ?
How many steps until collecting all types? Let ? be the number of coupons collected when the set first contains every type We ll see that: ? 1 ? ? ? = ? ?=1
Proof Let ?? be the number of collected coupons when the set first contains ? types By definition, ? = ?? Also: ??= ?1+ ?2 ?1 + + ?? ?? 1 ?? ?? 1 is a geometric random variable with success probability ? (? 1) Therefore: ? ? ? ? ? ? 1 1 ? ? ? = ? ?? ?? 1 = ? ? + 1= ? ? ? + 1= ? ?=1 ?=1 ?=1 ?=1
Hypercubes and the Ehrenfest Urn Model
Lazy Random Walk To fix the periodicity issue, we define a lazy random walk on the hypercube: Remain at current position with probability , otherwise pick a coordinate uniformly and flip the bit
A Slight Detour: Reversible Chains A distribution ? is reversible if: ?,? ?????= ????? This is called the detailed balance property A Markov chain is reversible if it has a reversible distribution Lemma: A reversible distribution is a stationary distribution
Proof ?11 ?21 ?31 ?41 ?12 ?22 ?32 ?42 ?13 ?23 ?33 ?43 ?14 ?24 ?34 ?44 ?1,?2,?3,?4 = ?1?11+ ?2?21+ ?3?31+ ?4?41, , , = ?11?1+ ?12?1+ ?13?1+ ?14?1, , , = ?1(?11+ ?12+ ?13+ ?14), , , = (?1, , , )
Stationary Distribution Any Markov chain which is defined by an undirected graph has the stationary distribution ?1 2?,?2 Proof: ?? 2? 2?, ,?? ? = 2? ?? 2?= 1 ?? =1 1 ?????= ????? ?? 2?
Back to Hypercubes The Hypercube graph is ?-regular: the degree of any node is ? So the stationary distribution is uniform
The Ehrenfest Urn There are ? balls, distributed among 2 urns At time ?, a ball is selected uniformly at random and moved from its current urn to the other Let ?? denote the number of balls in urn 1 at time ? The transition matrix: ? ?,? + 1 =? ? ? ? ?,? 1 =? ?
Stationary Distribution We ll show that the stationary distribution is binomial with parameters ? and : ? ? ? 1 2 ??= By verifying the useful detailed balance property (at least one case)
Detailed Balance Assuming ? = ? + 1, we need to show that: ?????= ????? ?,? So: ?? ? ?? ? ? 1 2 ? ? ?! 1 2 = ? ? + 1 ! ? ? 1 ! ? + 1 (? 1)! ?! ? ? 1 ! ? ?! ? ? ! ? ? ?! = ? ? (? 1)! ?! ? ? 1 !=
Tying it all together Let (??) be the simple random walk on the ?-dimensional hypercube Let ??= ?(??) be the Hamming weight of ?? When ??= ?: ??+1= ? + 1 when one of the ? ? coordinates with value 0 is selected ??+1= ? 1 when one of the ? coordinates with value 1 is selected Surprise: ? ?,? + 1 =? ? ? ? ?,? 1 =? ?
Groups A group (?, ) is a set with an associative operation ? ? ? and an identity member ?? ? such that: For all g ?, ?? ? = ? ?? = ? For all ? ?, there exists an inverse ? 1 ? s.t ? ? 1= ? 1 ? = ?? Given a probability distribution ? on a group ?, , we define a Markov chain with state space ? and transition matrix ? ?, ? = ? This is called the random walk on ? with increment distribution ?
Stationary Distribution The uniform probability distribution ? is a stationary distribution Proof: For any ? ?: 1 1 1 ? ? 1?,? = ? ?( ,?) = |?| |?| ?(?) = |?|= ?(?) ? ? ? ? ? ? = ? 1
Generating Sets A subset ? ? generates ? if every element of ? can be written as a product of elements of ? and their inverses We ll prove that: ?? is irreducible S = ? ? | ? ? > 0 generates ? We limit ourselves to finite groups
Proof () For any ? ?, since the random walk is irreducible, there exists ? > 0 such that ????,? > 0 Therefore, there is a sequence such that ? = ???? 1 ?1 and ?? ? So any ? ? can be expressed as a product of elements of ?
Proof () For any ?,? ?, ?? 1 can be written as a product of elements in S and their inverses Since every element of ? has finite order, any inverse ? 1 can be rewritten as ?? for some ? This sequence defines the set of steps which can be done to reach from ? to ?
Symmetric Probability Distribution ? is a symmetric probability distribution if for every ? ?: ? ? = ? ? 1 Proposition: the random walk ?? is reversible if ? is symmetric Proof: We know that the uniform distribution ? is stationary. From the detailed balance property: ? ? 1 and ? ? ,? = ? ? 1 ? ? ? ?, = |?| |?| These are equal if and only if ? ? 1= ? ? 1 1
Introduction We ll focus on nearest-neighbor random walk on : ? ?,? + 1 = ?, ? ?,? = ?, where ? + ? + ? = 1 ? ?,? 1 = ? Simple walk is defined as ? = ? =1 2,? = 0
Will the Chain Reach 0? Denote the first time the walk hits zero by ??= min ? 0 ??= 0 We ll prove: ???0> ? 12? ? For any integers ?,? > 0
Lemma 1 (Reflection Principal) For any positive integers ?,?,?: ???0< ?,??= ? = ????= ? When starting from ?, the probability of reaching 0 in ? steps and finishing in ? is equal to the probability of reaching ? ? ? ? 0
Proof Assume we reached 0 in exactly ? steps ???0= ?,??= ? = ???0= ? ?0?? ?= ? Symmetry when starting at 0: = ???0= ? ?0?? ?= ? = ???0= ?,??= ? And sum over all ? < ? to obtain ???0< ?,??= ? = ????= ? Sum over all ?: ???0< ?,??> 0 = ????< 0
Lemma 2 For any ? > 0: ???0> ? = ?0 ? < ?? ? The probability to reach 0 in more than ? steps when starting from ?, equals the probability to end in ?,? after ? steps when starting in 0
Proof ???0> ? = ?0 ? < ?? ? Condition on the time to reach 0: ????> 0 = ????> 0,?0 ? + ???0> ? From Lemma 1: ????> 0,?0 ? = ????< 0 From the symmetry of the walk: ????< 0 = ????> 2? So: ???0> ? = ????> 0 ????> 2? = ??0 < ?? 2? = ?0 ? < ?? ?
Lemma 3 3 ?0??= ? ? We ll prove by splitting to two cases: ? = 2? and ? = 2? + 1 The constant 3 is not very tight, but if it s good enough for Levin, Peres & Wilmer it s definitely good enough for me
3 Proof (Case ? = 2?) ?0??= ? ? ?2? must be an even number: ?2?= 2? To get to 2? we have to take ? + ? up moves and ? ? down moves, and the probability is This is maximized at ? = 0, so: 2? ?+?2 2? 2? 2? ! ?!222? 8 ? 1 2 2?= ?0?2?= 2? ? + ? 2? Stirling s formula 3 ?
3 Proof (Case ? = 2? + 1) ?0??= ? ? ?2?+1 must be an odd number: ?2?+1= 2? + 1 Condition on the first step to get: ?0?2?+1= 2? + 1 =1 2?1?2?= 2? + 1 +1 2?0?2?= 2? + 2 1 1 2 2? 1?2?= 2? + 1 8 ? =1 2?0?2?= 2? +1 1 2?+1 8 ? 1 2 2 2? 8 ? 1 2? + 1 2? 2 8 ? 1 4 1 3 = 2? + 1 2? + 1 ? 2? + 1 ? 1 2 2 ? ? 1
Tying it all together 12? ???0> ? = ?0 ? < ?? ? ? Lemma 2 Lemma 3
The Ballot Theorem We have two candidates, ? and ? The final vote count is ? and ? respectively, ? < ? At each step, we process one vote What is the probability that the winning candidate was always ahead?
Analysis We know we started from 0,0 and reached (?,?) after ? + ? votes Exactly ?+? ? such paths If ? was always ahead, we never reached the line ? = ? after (0,0) So the first step was up: ?+? 1 ? 1 paths How many of these reached the line later?
The Reflection Property Take a path which started with up , touched ? = ? and ended at (?,?) Reflect the portion after the first touch of ? = ? Now a path from (0,0), starting up , ending at (?,?) Any such path must cross ? = ? Therefore: ?+? 1 ? bad paths we need to subtract
Final Details There are ?+? 1 Out of them, ?+? 1 The total number of paths is ?+? paths which started with up and reached ?,? ? 1 are bad paths we need to subtract ? ? ?+? 1 ? 1 ?+? 1 ? ?!?! ? + ? ! ? + ? 1 ! ?! ? 1 ! ? + ? 1 ! (? 1)!?! = ?+? ? ? ? + ?=? ? ? = ? + ? ? + ?