Mastering Algebraic Methods with Simplification Worked Examples
Explore algebraic methods including algebraic fractions, dividing polynomials, the factor theorem, mathematical proofs, and methods of proof through various worked examples for simplification. Enhance your understanding and skills in algebra with step-by-step solutions provided.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
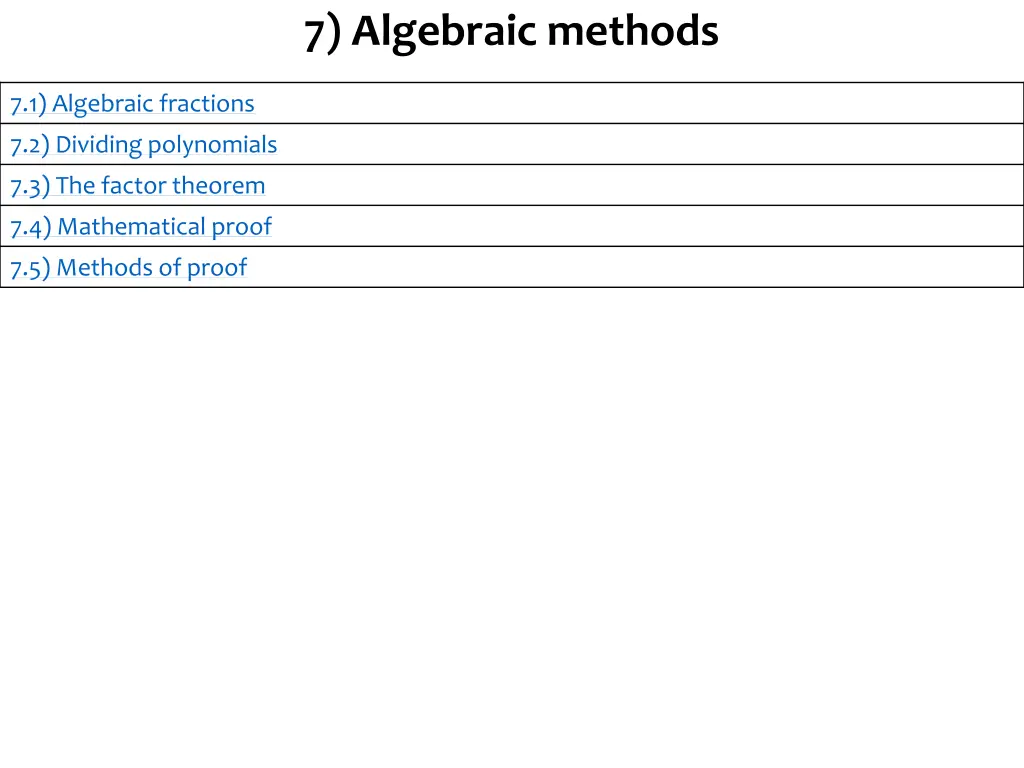
7) Algebraic methods 7.1) Algebraic fractions 7.2) Dividing polynomials 7.3) The factor theorem 7.4) Mathematical proof 7.5) Methods of proof
Chapter CONTENTS 7.1) Algebraic fractions
Your turn Worked example Simplify: ?3 ? Simplify: ?4 ? 8?7 12?3 2?4 3 ?4 ?2 6?4 ?2 9?5 15?9 3 5?4 6?5 2?2 6?5 8?2 6?5 12?2 6?5 18?8
Your turn Worked example Simplify: Simplify: ?2+ ? 6 9 ?2 4 ?2 ?2+ 2? 8 ? + 2 ? + 4
Your turn Worked example Simplify: Simplify: 2?4 7?3 4?2 3?7 6?3?9 28?3? 3?2 5?3 4? 2?5 10?? 2?3 3?5 ?4 5?2 6?2?3
Your turn Worked example Simplify: Simplify: ? 3 4? 12 1 4 5? + 10 ? + 2 ? 7 5? 35
Your turn Worked example Simplify: Simplify: ?2+ 5? + 6 ? + 2 ?2 7? + 10 3? 15 ? 2 3 4? 12 ?2 5? + 6
Your turn Worked example Simplify: Simplify: ? + 3 ? + 33 ? 52 ? 56 1 ? 54 ? 45 ? 42 ? + 53 3? + 15 ? + 52 3 2? + 10 ? + 57
Your turn Worked example Simplify: Simplify: 3?2+ 6? 15? 4?3+ 12? 16?2 ?2+ 3 4? 5?2 30?4 10?3
Your turn Worked example Simplify: Simplify: ?2+ 6? + 5 ?2+ 3? 10 ?2 6? + 5 ?2+ 4? 5 ? 5 ? + 5 ?2 7? 8 ?2 1
Your turn Worked example Simplify: Simplify: 2?2 5? 3 3?2 11? + 6 3?2 5? 2 2?2 7? + 6 3? + 1 2? 3 3?2 ? 10 ?2 4
Your turn Worked example Simplify: Simplify: ?2 1 ? + 1 2? + 8 ?2 16 2 ? 4 ? 2 ?2 4 ?2 9 2? 6
Your turn Worked example Simplify: Simplify: ? + 2 ? 3 ? 3 3? 4 ? + 2 5? + 10 ? 2 3? + 4 5 3? 4 3? + 4 2? + 3 ? 4 2? 8 2? + 1
Your turn Worked example Simplify: Simplify: ? + 2 ? 3 ? 2 3? 4 ? + 2 5 3? 4 3? + 4 3? + 4 5? + 10 ? 3 2? + 3 ? 4 2? + 1 2? 8
Your turn Worked example Simplify: ? + 2 3? 4 ? 5 6? + 7 Simplify: ? + 5 2? 7 ? 4 3? + 1 7? + 6 ? 5 4? 3 ? + 2 6? + 1 ? 4 2? 9 ? + 3 ? + 5 2? 7 6? + 1 3? + 1 2? 9 ? + 3 ? + 7 6? 5 ? 4 3? + 2 ? + 4 3? + 2 6? + 5 7?
Your turn Worked example Simplify: 6?2+ 37? 35 ?2 3? 4 Simplify: 3?2 10? 8 2?2 7? 15 3?2+ 10? 8 2?2+ ? 3 ?2 49 ?2 16 ? 5 ? 4 3? 2 ? 1
Your turn Worked example Simplify: Simplify: 2?3 5?2 3? 2? 6 3?3 ?2 10? 4? 8 ? 3? + 5 4
Your turn Worked example Simplify: Simplify: 2?3+ 5?2 3? 4?2 1 3?3 ?2 10? 9?2 25 ? ? 2 3? 5
Your turn Worked example Write as a single fraction: Write as a single fraction: 3 5 5 3 + ? + 2 2? 1 5? + 7 ? + 2 3 2 5? + 4
Your turn Worked example Write as a single fraction: 3 (? 4) ?2 16 Write as a single simplified fraction: 5 (? 2) ?2 4 ? 5 ? + 3 4? 13 ? 2
Your turn Worked example ? ? Write in the form 1 + Write in the form 1 + ?+?: ?+?: ? + 3 ? 5 ? 5 ? + 2 7 1 ? + 2 ? 2 ? + 7
Your turn Worked example Simplify: Simplify: 3 ?+ 2 1 +5 5 3?+ 3 7 +2 ? 3? 9? + 5 21? + 2 3 2? 2 1 5 2?
Chapter CONTENTS 7.2) Dividing polynomials
Your turn Worked example Divide ?3 2?2 17? + 10 by (? 5) Divide ?3+ 2?2 17? + 6 by (? 3) ?2+ 5? 2
Your turn Worked example ? ? = 18?4 29?2+ 3 Divide ?(?) by (3? + 1). Give your answer in the form ? ? = (3? + 1)(??3+ ??2+ ?? + ?) ? ? = 4?4 17?2+ 4 Divide ?(?) by (2? + 1). Give your answer in the form ? ? = (2? + 1)(??3+ ??2+ ?? + ?) ? ? = (2? + 1)(2?3 ?2 8? + 4)
Your turn Worked example Find the remainder when 2?3+ 5?2 10? + 16 is divided by (? 2) Find the remainder when 2?3 5?2 16? + 10 is divided by (? 4) 6
Your turn Worked example Divide 27?3 8 by 3? 2 Divide 8?3 1 by 2? 1 4?2+ 2? + 1
Your turn Worked example ? ? = 6?3+ 11?2 46? + 24 Show that (3? 2) is a factor of ?(?) and hence find all the real roots of the equation ? ? = 0 ? ? = 12?3 14?2 61? + 60 Show that (2? 3) is a factor of ?(?) and hence find all the real roots of the equation ? ? = 0 ? = 5 2,? =3 2,? =4 3
Chapter CONTENTS 7.3) The factor theorem
Your turn Worked example Show that (? 3) is a factor of ?3 2?2 5? + 6 Show that (? 2) is a factor of ?3+ ?2 4? 4 Shown (e.g. algebraic division or factor theorem)
Your turn Worked example Fully factorise 3?3+ ?2 12? 4 Fully factorise 2?3+ ?2 18? 9 (? 3)(2? + 1)(? + 3)
Your turn Worked example Given that ? + 2 is a factor of 3?4 4?2+ ?, find the value of ?. Given that ? + 1 is a factor of 4?4 3?2+ ?, find the value of ?. ? = 1
Your turn Worked example Given that 3? + 1 is a factor of 12?3+ ??2+ 2, find the value of ?. Given that 2? + 1 is a factor of 6?3+ ??2+ 1, find the value of ?. ? = 1
Your turn Worked example Given that 2? 1 is a factor of 2?3+ 3?2+ ?? + 11, find the value of ?. Given that 3? 1 is a factor of 3?3+ 11?2+ ?? + 1, find the value of ?. ? = 7
Your turn Worked example Show that (? 2) is a factor of 5?4 16?3 47?2+ 130? 24 and hence find all the real solutions to 5?4 16?3 47?2+ 130? 24 = 0 Show that (? 3) is a factor of 4?4+ 15?3 48?2 109? + 30 and hence find all the real solutions to 4?4+ 15?3 48?2 109? + 30 = 0 ? = 5,? = 2,? =1 3,? = 3
Chapter CONTENTS 7.4) Mathematical proof
Your turn Worked example Prove that 2? 3 ? 7 ? + 5 2?3 7?2 64? + 105 Prove that 3? + 2 ? 5 ? + 7 3?3+ 8?2 101? 70 Proof
Your turn Worked example Prove that if three consecutive even integers are the sides of a right-angled triangle, they must be 6, 8 and 10. Prove that if three consecutive integers are the sides of a right-angled triangle, they must be 3, 4 and 5. Proof e.g. Pythagoras Theorem with ?,? + 1,? + 2
Your turn Worked example Prove that ?2+ 6? + 11 is positive for all values of ?. Prove that ?2+ 4? + 5 is positive for all values of ?. ?2+ 4? + 5 = ? + 22+ 1 ?2 0 ? + 22 0 ? + 22+ 1 1
Your turn Worked example Prove that the sum of the squares of two consecutive even numbers is 4 more than a multiple of 8. Prove that the sum of the squares of two consecutive odd numbers is 2 more than a multiple of 8. Proof
Your turn Worked example Prove that (1,1), (4,7) and (10,4) are the vertices of a right-angled triangle. Prove that (1,1), (3,3) and (4,2) are the vertices of a right-angled triangle. Proof e.g. Pythagoras Theorem or perpendicular gradients AB and BC
Your turn Worked example The equation ??2+ 5?? + 3 = 0, where ? is a constant, has no real roots. Prove that ? satisfies the inequality 0 ? < 12 25 The equation ??2+ 3?? + 2 = 0, where ? is a constant, has no real roots. Prove that ? satisfies the inequality 0 ? <8 9 Proof
Your turn Worked example Prove that 4? 3 + 2? + 7 is a multiple of 2 for all real integers ? Prove that 4? 3 + 10? 11 is a multiple of 7 for all real integers ? 14? 14 7 2? 2 7? Prove that 4? 3 + 2? 9 is a multiple of 3 for all real integers ?
Your turn Worked example Prove that the sum of five consecutive integers is a multiple of 5. Prove that the sum of three consecutive integers is a multiple of 3. Let the first integer be ?: ? + ? + 1 + ? + 2 3? + 3 3 ? + 1
Your turn Worked example Prove that the product of two odd numbers is an odd number. Prove that the product of two even numbers is an even number. Let even numbers be 2? and 2?: 2? 2? 4?? 2 2??
Your turn Worked example Prove algebraically that ?2 2 ? 22 is always even, given ? is an integer greater than 1 Prove algebraically that 2? + 12 (2? + 1) is an even number 2? + 12 2? + 1 4?2+ 4? + 1 2? 1 4?2+ 2? 2 2?2+ ?
Your turn Worked example Prove that ? 12+ ?2+ ? + 12 is two more than a multiple of 3 for all positive integer values of ? Prove that ? + 12 ?2 is one more than a multiple of 2 for all positive integer values of ? ? + 12 ?2 ?2+ 2? + 1 ?2 2? + 1
Your turn Worked example Prove that 2? + 32 2? 32 is a multiple of 8 for all positive integer values of ? Prove that 3? + 22 3? 22 is a multiple of 8 for all positive integer values of ? 9?2+ 12? + 4 9?2 12? + 4 9?2+ 12? + 4 9?2+ 12? 4 24? 8 3? 3? + 22 3? 22
Your turn Worked example Prove algebraically that the difference between two different odd numbers is an even number. Prove algebraically that the difference between two different even numbers is an even number. Let even numbers be 2? and 2?: 2? 2? 2 ? ?
Your turn Worked example Prove that the product of four consecutive integers is always a multiple of 8 Prove that the product of three consecutive integers is always a multiple of 6 Proof by showing at least one is a multiple of 2, and one will be a multiple of 3