Mastering Exponents in Mathematics

Everything I know About Everything I know About Exponents! Exponents! By: Madelaine Wong

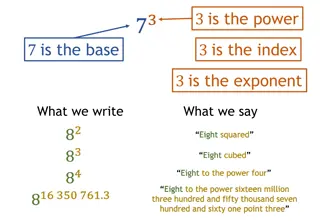
P.L.Os for Exponents P.L.O s for Exponents 1. 1. Represent repeated multiplication with exponents Represent repeated multiplication with exponents Powers are basically repeated multiplication simplified. Instead of writing 2x2x2x2x2, you can simply write 25which instantly makes things easier, faster and neater. Another example is 6x6x6x6x6x6 = 66 2. Describe how powers represent repeated multiplication 2. Describe how powers represent repeated multiplication It is like the learning outcome above, just reversed, 25 = 2x2x2x2x2 3. Demonstrate the difference between the exponent and the base by building 3. Demonstrate the difference between the exponent and the base by building models of a given power, such as models of a given power, such as ?? and and ?? The base, which is X in ??, is simply the number that is being multiplied many times by itself (ex. X = 2 if the equation was 2x2x2x2x2). The exponent or n in ??is the number of times you multiply the base by itself (ex. 2x2x2x2x2 ?? X = 2 N =5 25) So, if we were to build a model, 23could be shown as a cube with it s length, width and height all represented by 2 units. To find the volume of the cube we would have to do LxWxH = 23 because we multiply 2, 3 times by itself. 32 can be modeled as the area of a 2D square which is LxW. 3 would be the units and 2 would be the number of times

Demonstrate the difference between two given powers in which the exponent Demonstrate the difference between two given powers in which the exponent and the base and interchanged by using and the base and interchanged by using 23 & 32 23 = 2x2x2 whereas 32 = 3x3 23can be modeled as a cube with the measurement is 2 units. 32 can be modeled as a 2D square Evaluate powers with integral bases (excluding base 0) and whole number Evaluate powers with integral bases (excluding base 0) and whole number exponents exponents Ex. 54= 5x5x5x5 = 625. Powers with a positive base and a positive exponent will have a positive result. Powers that have a negative base might have a negative or positive result, depending on where the brackets are. Explain the role of parentheses in powers by evaluating a given set of powers Explain the role of parentheses in powers by evaluating a given set of powers such as such as 24, 24 & 24 In example number one, 24, the brackets mean that the base will be multiplied with that sign, which is negative in this case. When you write it out in repeated multiplication form, it will be (-2)(-2)(-2)(-2). If you re dealing with a negative base and an even exponent, the answer will be positive, however if the exponent is an odd number, the result will be negative because there s not enough negatives to cancel them out completely. When we have something like 24, it will be written as (-1x2x2x2x2) You are still writing out the 24 but we put the negative sign with a one and times that with the result = 1 24. 24is pretty much the same as the example before, it s written the same except this time the equation will look like this; 1 2 2 2 2

Explain the exponent laws for Explain the exponent laws for multiplying and dividing powers with multiplying and dividing powers with the same base the same base Explain the laws for a power with the Explain the laws for a power with the exponent zero exponent zero Whenever there is a power with the exponent zero, the result will always be one. This law works with the base as any number, however the base cannot be zero. The product law is used for exponents that are being multiplied together with the same base. 1) You keep the base 2) You add the exponents together 3) If there s a coefficient you multiply them together. For example, 2 72 3 73 = 3x2 72+3 = 6 75 then you solve! ?0= 1 ? 0 Use patterns to show that a power Use patterns to show that a power with the exponent zero is equal to with the exponent zero is equal to one one 23= 8,22= 4,21= 2,20= 1 The quotient law is similar to the product. 1) You keep the base 2) Subtract the exponents 3) Divide the coefficients if there are any. In example, 6 25 2 23 =6 2 25 3 = 3 22 Easy! In the pattern above, each time the exponent decreases by one, you divide the result by two. That s why 20= 1 because you divide 21= 2 by 2 the result is one. Same goes for any other power with a variety of bases. Instead, just every time the exponent decreases by one, you divide the previous results by the base. Explain the exponent laws for raising Explain the exponent laws for raising a product and quotient to an a product and quotient to an exponent exponent This is the power law for raising a product and quotient to a exponent. 1) keep the base 2) Multiply the exponents together 3) Apply the exponent to the coefficient, only if the coefficient is in the brackets. A lot of people forget to apply the exponent to the coefficient. 3 4 32 3= 4 36 or 4 32 =4 729 =43(36) =64(729) =2916 = 46656

Explain the laws for powers with Explain the laws for powers with negative exponents negative exponents The negative exponent law is used when there is a negative exponent with a power. If the negative exponent is in the top or numerator, we flip is so it s at the bottom and vice versa. For example ? 2?3 I can apply the exponent I can apply the exponent laws to powers with both laws to powers with both integral and variable integral and variable bases bases 3 24= 3 16 = 48 ? 4=?3?4 32=1 ?2or if it s just a 1 9 single power like 3 2= ? 2?3 ?2 ? ?2 = Use patterns to explain the negative Use patterns to explain the negative exponent law exponent law ?3? 4? 2 ?3 3 I can identify the error I can identify the error simplification of an simplification of an expression involving expression involving powers powers 5 32+ 73 152+ 73 225 + 343 = 568 WRONG! 5?32+ 73 5 9 + 73 40 + 343 = 383 ?3 = = ?3 3???2 1 23x1 33=1 8x1 1 2 3 3 3= 9= 72

Use the order of operations on expressions with Use the order of operations on expressions with powers powers All you do is follow BEDMAS and follow the equation from left to right. 32+ 6 2 x 23 9 + 3 8 12 8 = 96 Determine the sum and difference of two powers Determine the sum and difference of two powers Just follow BEDMAS! 43+ 33 64 + 27 = 91 53 62 125 36 = 89

Identify the error of applying the order of Identify the error of applying the order of operations in an incorrect solution operations in an incorrect solution 2 + 3 232 + 3 23 =5 23 WRONG! Didn t follow BEDMAS properly =2 + 3 8 = =103 = 1000 Use powers to solve problems (measurement Use powers to solve problems (measurement problems) problems) In this unit we ve worked with Pythagoreans' Theorem (?2+ ?2= ?2) & figuring out the side length of a square with a given area. = 2 + 24 = 26

Use powers to solve problems (growth problems) Use powers to solve problems (growth problems) Bacteria triples every hour, you start with 30. How many after 2 hours? 5? 7? n? Hr.1 = 30 Hr.7 = 30 x 37= 65 610 Hr.2 = 30 x 3 = 90 Hr.n = 30 x 3? Hr.5 = 30 x 35 = 7290 Applying the order of operations on expressions with powers involving negative Applying the order of operations on expressions with powers involving negative exponents and variable bases exponents and variable bases Just follow BEDMAS and the exponent laws if applicable ? 3?2 ?2? 3 = ? 5?5 = ?5 ?5