Mastering Linear Inequalities: Techniques and Visual Representations
Explore the world of linear inequalities with Dr. J. Frost in Year 9, covering topics such as solving, combining, and representing solutions on number lines. Learn about strict inequalities, manipulating inequalities, flipping the inequality when multiplying or dividing by negatives, and alternative approaches to avoid division by negative numbers. Enhance your understanding with visual tools and interactive activities. Get ready to excel in solving linear inequalities!
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Year 9 Inequalities Dr J Frost (jfrost@tiffin.kingston.sch.uk) Objectives: Solving linear inequalities, combining inequalities and representing solutions on number lines. Last modified: 23rd March 2015
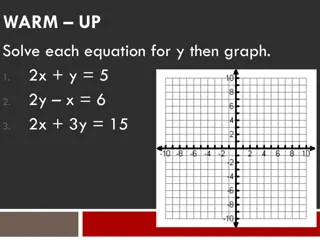
Writing inequalities and drawing number lines You need to be able to sketch equalities and strict inequalities on a number line. This is known as a strict inequality. x > 3 x < -1 ? Means: x is (strictly) greater than 3. ? Means: x is (strictly) less than -1. 0 1 2 3 4 5 -3 -2 -1 0 1 2 ? ? x 4 x 5 ? ? Means: x is greater than or equal to 4. Means: x is less than or equal to 4. 2 3 4 5 6 7 2 3 4 5 6 7 ? ?
Deal or No Deal? We can manipulate inequalities in various ways, but which of these are allowed and not allowed? ? > ? Can we add or subtract to both sides? ? ? > ? Click to Deal Click to No Deal
Deal or No Deal? We can manipulate inequalities in various ways, but which of these are allowed and not allowed? ?? > ? Can we divide both sides by a positive number? ? > ? Click to Deal Click to No Deal
Deal or No Deal? We can manipulate inequalities in various ways, but which of these are allowed and not allowed? ? < ? Can we multiply both sides by a positive number? ?? < ? Click to Deal Click to No Deal
Deal or No Deal? We can manipulate inequalities in various ways, but which of these are allowed and not allowed? ? < ? Can we multiply both sides by a negative number? ? < ? Click to Deal Click to No Deal
Flipping the inequality If we multiply or divide both sides of the inequality by a negative number, the inequality flips ! OMG magic! 2 -2 -4 < 4 Click to start Bro-manimation
Alternative Approach Or you could simply avoid dividing by a negative number at all by moving the variable to the side that is positive. 1 3? 7 1 7 3? 6 3? 2 ? ? 2 ? < 3 3 < ? ? > 3 ? ? ? ? ? ?
Quickfire Examples Solve 2? < 4 ? < 2 ? Solve ? < 3 ? ? > 3 Solve ? 3 ? 4? 12 Solve 4? > 4 ? 2 1 ? < 1 ? Solve ? 2 ?
Deal or No Deal? We can manipulate inequalities in various ways, but which of these are allowed and not allowed? 1 ?< 2 Can we multiply both sides by a variable? 1 < 2? Click to Deal Click to No Deal The problem is, we don t know if the variable has a positive or negative value, so negative solutions would flip it and positive ones wouldn t. You won t have to solve questions like this until Further Maths A Level!
More Examples Hint: Do the addition/subtraction before you do the multiplication/division. Solve 3? 4 < 20 ? < 8 ? Solve 4? + 7 > 35 ? > 7 ? 5 +? Solve ? 14 ? 2 2 Solve 7 3? > 4 ? < 1 ? Solve 6 ? ? 15 ? 3 1
Dealing with multiple inequalities Hint: Do the addition/subtraction before you do the multiplication/division. 8 < 5x - 2 23 8 < 5x - 2 5x - 2 23 and 2 < x and x 5 2 < x x 5 ? < ? ? Click to start bromanimation
More Examples Hint: Do the addition/subtraction before you do the multiplication/division. Solve ? < ? < ? ? ? < ?? + ? < ? Solve ? < ? < ? ? < ? < ? ?
Test Your Understanding Solve ? < ? < ? ? ?? < ?? ? < ?? Solve ? < ? ?? < ? ? < ? < ? ?
Exercise 1 Solve the following inequalities, and illustrate each on a number line: Sketch the graphs for ? =1 ? and ? = 1. Hence solve 1 0 < x < 1 ? 1 ?> 1 2? 1 > 5 2? < 4 5? 2 3? + 4 ? 4+ 1 6 ? 6 1 7 1 ? 2 1 4? > 5 5 2? 1 < 9 5 1 2? < 9 10 + ? < 4? + 1 < 33 ? < ? < ? 1 3? < 2 2? < 3 ? ? > ? ? > ? ? ? 1 ? ? 2 3 ? You can get around the problem of multiplying/dividing both sides by an expression involving a variable, by separately considering when it s positive, and when it s negative, and putting this together. Hence solve: 3 ? + 2> 4 If we assume ? + ? is positive, then ? > ? and solving gives ? < ? ? < ? ? as we had to assume ? > ?. If ? < ? then this solves to ? > ? is a contradiction. Thus ? < ? < ? ? 2 4 ? ?? ? 5 ? ?? ? ? ? ? ? ? 6 ? 7 ? < ? ? ? < ? ? < ? ? ? ? 8 ?. Thus ? < 9 ? 10 ? ? which ? > ? ? 11
Combining inequalities It s absolutely crucial that you distinguish between the words and and or when constraining the values of a variable. How would we express x is greater than or equal to 2, and less than 4 ? How would we express x is less than -1, or greater than 3 ? AND OR x < -1 or x > 3 ? x 2 and x < 4 ? x 2, x < 4 ? This is the only way you would write this you must use the word or . 2 x < 4 ? This last one emphasises the fact that x is between 2 and 4.
Combining inequalities It s absolutely crucial that you distinguish between the words and and or when constraining the values of a variable. 2 x < 4 x < -1 or x > 4 0 1 2 3 4 5 -1 0 1 2 3 4 ? ?
Combining inequalities It s absolutely crucial that you distinguish between the words and and or when constraining the values of a variable. To illustrate the difference, what happens when we switch them? or and x 2 and x < 4 x < -1 or x > 4 0 1 2 3 4 5 -1 0 1 2 3 4 ? ?
I will shoot you if I see any of these 4 > ? < 8 This is technically equivalent to: x < 4 ? This is technically equivalent to: x > 7 ? 4 < ? > 7 The least offensive of the three, but should be written: 4 < x < 7 ? 7 > ? > 4
Combining Inequalities In general, we can combine inequalities either by common sense, or using number lines... 2 5 Where are you on both lines? 4 Combined ? ? > ? 2 5 2 < ? < 5 4 ? < 4 Combined ? < ? < ? ?
Test Your Understanding ? -1 5 1st condition ? -3 3 ? 2nd condition ? Combined
Exercise 2 By sketching the number lines or otherwise, combine the following inequalities. ? ??? 1 2 3 4 ? ? 5 6 7 8 9 10 ? ?? ? ? ? ? 11 12 13 14 ? 15 ?