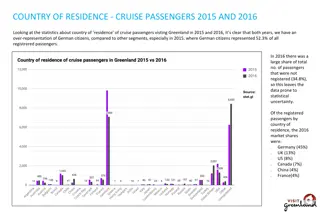
Mastering Mathematics and The New Primary Curriculum Insights
Gain valuable insights into mastering mathematics and navigating the new primary curriculum. Explore concepts such as differentiation, mastery approach, and the role of intelligence in learning.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Mike Askew MASTERING MATHEMATICS & THE NEW PRIMARY CURRICULUM info@mikeaskew.net @mikeaske26 www.mikeaskew.net
info@mikeaskew.net www.mikeaskew.net @mikeaskew26 2
Maths is NOT a spectator sport
What if You tried to create as many layers as possible? You changed the shape? You used fractions? You modelled what is going on on a number line?
Is learning based in Intelligence which we have in different quantities? Actions and communication which we can all engage in?
Differences Aptitude Attainment Experience
Container view of ability
Container view of ability
Developmentally plastic
Differentiation Between and within class grouping Differentiation results in pupils engaging with different curricula.
Should the curriculum be changed to meet individual needs? kept constant and made accessible to all?
Mastery (Bloom) Feedback Range of experiences Depth
Mastery approach Expectation that almost everyone can master most of the curriculum Moving through the curriculum at the same pace Spending longer on fewer topics Differentiating support Depth of understanding
Start with Mathematics Product Mathematising Process, especially reasoning
Variation & Reasoning A 9 litre vat of jam is used to fill some 3 litre jars. How many jars can be filled? A 9 litre vat of jam is used to fill some 1 litre jars. How many jars can be filled? A 9 litre vat of jam is used to fill some 1/2 litre jars. How many jars can be filled? A 9 litre vat of jam is used to fill some 1/3 litre jars. How many jars can be filled?
Variation The relationship between examples is as important (if not more so) than the examples on their own.
Variation Key question: What is the same? What is different? Key to keep in mind When planning What directing learners attention
Mathematical reasoning, even more so than children s knowledge of arithmetic, is important for children s later achievement in mathematics. Nunes et al. DSFC RR-118
Pre-test Correct Post-test Correct 8 + 4 = [ ] + 5 9 + 3 = [ ] + 4 32 + 19 = [ ] + 20 44 + 19 = [ ] + 20 68 - 39 = [ ] - 40 56 - 19 = [ ] - 20
Pre-test Correct Post-test Correct 8 + 4 = [ ] + 5 58% 9 + 3 = [ ] + 4 32 + 19 = [ ] + 20 53% 44 + 19 = [ ] + 20 68 - 39 = [ ] - 40 56 - 19 = [ ] - 20
Pre-test Correct Post-test Correct 8 + 4 = [ ] + 5 58% 9 + 3 = [ ] + 4 32 + 19 = [ ] + 20 53% 44 + 19 = [ ] + 20 68 - 39 = [ ] - 40 26% 56 - 19 = [ ] - 20
Pre-test Correct Post-test Correct 8 + 4 = [ ] + 5 58% 9 + 3 = [ ] + 4 96% 32 + 19 = [ ] + 20 53% 44 + 19 = [ ] + 20 92% 68 - 39 = [ ] - 40 26% 56 - 19 = [ ] - 20 55%
Reasoning 39 68
Reasoning 39 68
Reasoning 39 68 ? 69
Reasoning 39 68 ? 69
Problem solving Learning to solve problems Learning through solving problems
Problem solving One problem, three solutions Teaching and learning begins after the problem is solved
Enabling conditions Valuing gesture, action, movement Power of imagination Wide variety of tools available Mathematically rich environment Safe, trusting climate Conditionality of approaches could Peer support and collaboration Dialogue