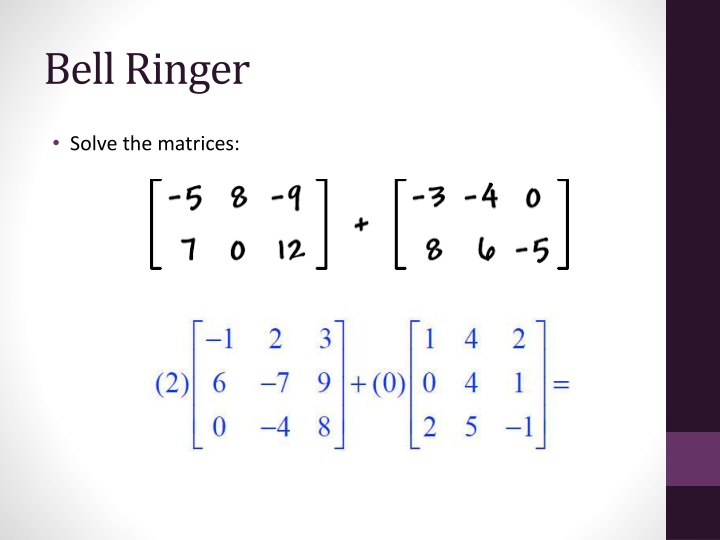Math Concepts: Matrices, Distributive Property, Like Terms, and More
Dive into essential math concepts such as matrices, distributive property, like terms, and additional properties of numbers. Learn about terms, coefficients, and how to combine like terms. Explore properties like commutative and associative, and understand the symmetric property. Enhance your math skills with practical examples and visuals.
Uploaded on Mar 10, 2025 | 1 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Bell Ringer Solve the matrices:
Distributive Property Mr. Haupt CC.2.1.8.E.1
Distributive Property The easiest definition is the multiplication of everything inside a set of parentheses by what is on the outside.
Some Important Words Term a term is a number, variable, or a combination of a number and a variable. For example: 3, b, 4x, -9y2 Constant a constant is a number with no variable attached. Coefficient a coefficient is a number attached to a variable and is what you multiply the variable by. For example: in 7g the coefficient is the 7 Like Terms like terms have the exact same variable factors. 7x and 3x are like terms, but 7x and 3x2are not
Like Terms Combine the like terms: 12 x + 7y 3x -6x2+ 4x + 13x2 4w + 6j 5w2 14b + 14c 8a2+ 7a 5b + 2c a2
Time to Distribute Simplify and combine like terms: 7(a + 4) 12b + 3(5 b) -5q q(4 + q) 16 + 3(7a + 2) 8(10 3a)
Additional Properties of Numbers Commutative Property of Addition Commutative Property of Multiplication Associative Property of Addition Associative Property of Multiplication Identity Property of Addition Identity Property of Multiplication Inverse Property of Addition Inverse Property of Multiplication Symmetric Property
Commutative Property of Addition a + b = b + a Example: 7 + 3 = 3 + 7
Commutative Property of Multiplication a * b = b * a Example: 3 * 7 = 7 * 3
Associative Property of Addition (a + b) + c = a + (b + c) Example: (6 + 4) + 5 = 6 + (4 + 5)
Associative Property of Multiplication (a * b) * c = a * (b * c) Example: (6 * 4) * 5 = 6 * (4 * 5)
Identity Property of Addition a + 0 = a Example: 8 + 0 = 8
Identity Property of Multiplication a * 1 = a Example: 8 * 1 = 8
Inverse Property of Addition For every a there is an additive inverse a so that a + (-a) = 0 Example: 4 + (-4) = 0
Inverse Property of Multiplication For every a that is not zero there is a multiplicative inverse, 1/a so that a(1/a) = 1 Example: 5 * 1/5 = 1
Symmetric Property If a = b then b = a Example: 2 * 3 = 6, so 6 = 2 * 3