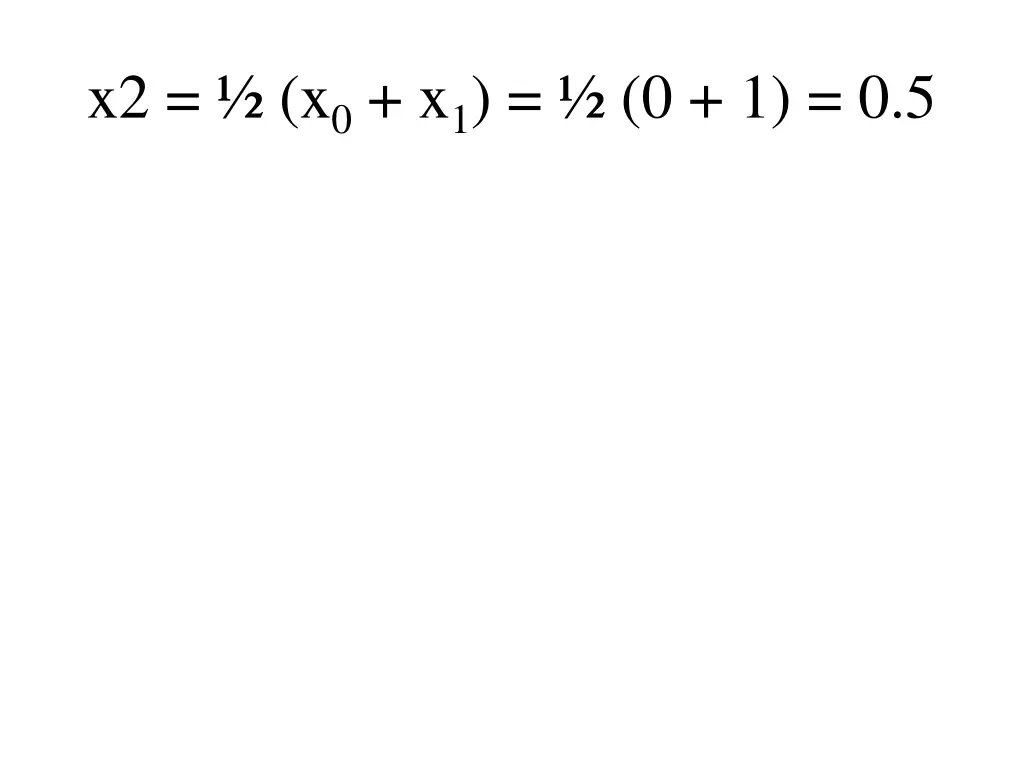
Mathematical Analysis of Variable Function Compositions

x2 x 0 x 1 0 1 0 5 n.w
1 / 133
Embed
Share

Explore the step-by-step calculations involving various mathematical functions with neglecting and rejecting certain variables. Discover the outcomes of function compositions and their values at specific inputs. Follow the progression through a series of mathematical operations to understand the results obtained.

  • Mathematics
  • Function Compositions
  • Variable Analysis
  • Mathematical Operations
rayaanacharya
moxl_752 Follow

Uploaded on | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

Download Presentation

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

E N D

Presentation Transcript

  1. x2 = (x0+ x1) = (0 + 1) = 0.5

  2. F(0.5) = -0.25 is ve

  3. We neglect x1and we have

  4. X3 = (x0+ x2) = (0 + 0.5) = 0.25

  5. F(0.25) = 0.3125 ve

  6. We neglect x0and we have

  7. x4= (x2+ x3) = (0.5 + 0.25) = 0.375

  8. F (0.375) is +ve

  9. We reject x3and we have

  10. x5= (x2+ x4) = (0.5 + 0.375) = 0.4375

  11. F(0.4375) is ve

  12. We reject x2, and have

  13. x6= (x4+ x5) = (0.375 + 0.4375)

  14. F(x0) = +1

  15. F(x1) = -1

  16. X0= 9nx1= bn (x0+ x1) F (cn) 0

  17. 0

  18. 0.5

  19. 0.5

  20. 0.375 1

  21. 0.5

  22. 0.25

  23. 0.375

  24. 0.4375 0.5

  25. 0.25

  26. 0.375

  27. 0.4375

  28. 0.40625-0.25 ve

  29. 0.3125 +ve

  30. 0.0156 +ve

  31. -0.12109 -ve

  32. This is linear function x(y) with x(y0) = x0and x(y1) = x1

  33. The line intersects the x axis at the point obtained by putting y = 0 in (3.4)

  34. -y1 -y0

  35. y0 y1 y1 y0

  36. = x0y1 x1y0

  37. y1 y0

  38. This may be re-written on a linear interpolation form as x0F(x1) x1 F(x0)

  39. F(x1) F(x0)

  40. This can also be written as

  41. X2= x1 (x1 x0) F (x1)

  42. F (xi) F(x0)

  43. iterative scheme results. As in the case of binary search (bisection rule) the two estimates slid give opposite signs in F(x).

  44. The convergence in this method is faster than that in bisection rule.

  45. Example F(x) = x2 3x + 1 = 0

  46. Choose x0= 0

  47. x1= 1

  48. Since F(x0) is +ve = 1

Related


No related presentations.

More Related Content