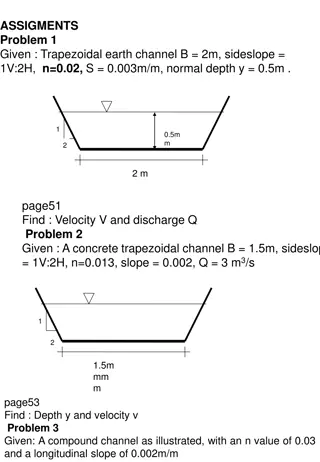
Micromechanical Analysis of Lamina Elastic Moduli in Composite Materials
Micromechanical analysis of lamina elastic moduli in composite materials, focusing on properties like longitudinal elastic modulus, transverse elastic modulus, Poisson's ratio, and in-plane shear modulus. It explains how to calculate the longitudinal Young’s modulus for a unidirectional lamina and provides insights on the load distribution between fibers and the composite material. A specific example involving a Glass/Epoxy lamina with a 70% fiber volume fraction is used to demonstrate the calculations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Chapter 3 Micromechanical Analysis of a Lamina Elastic Moduli of Unidirectional Lamina Dr. Autar Kaw Department of Mechanical Engineering University of South Florida, Tampa, FL 33620 Courtesy of the Textbook Mechanics of Composite Materials by Kaw
Longitudinal elastic modulus, ?1 Transverse elastic modulus, ?2 Major Poisson s ratio, ?12 In-plane shear modulus, ?12
3 2 1 ???? ???? = ?? ?? ??= h ??= ???? ???? = ?? ?? tc Lc h tm/2 FIGURE 3.3 Representative volume element of a unidirectional lamina. tf tm/2 tc
h c c tm/2 tf tm/2 tc FIGURE 3.4 A longitudinal stress applied to the representative volume element to calculate the longitudinal Young s modulus for a unidirectional lamina.
= c = f F , and , A m = m F A F = c F + f F c c m F A f f m h c c tm/2 tf = c , tm/2 E = f E f tc 1 c , and f m E = m m
E = c E + f c = E A A A then ), 1 f m m c f m If ( : f = m A A f m E = 1 E + c E f m A A c E = 1 V f E + f V m E m
E = 1 V f E + f V m E = f E m = c , and , E f = c = f A , and , = 1 c F A c c F f f f m E = m F A m m m m F E f f = V 1 f F E c
F E f f = V 1 f F E c FIGURE 3.5 Fraction of load of composite carried by fibers as a function of fiber volume fraction for constant fiber to matrix moduli ratio.
Find the longitudinal elastic modulus of a unidirectional Glass/Epoxy lamina with a 70% fiber volume fraction. Use the properties of glass and epoxy from Tables 3.1 and 3.2, respectively. Also, find the ratio of the load the fibers take to that of the composite. Ef = 85 GPa Em = 3.4 GPa E = 1 V f E + f V m E m ( ( ) + ) 3.4 ( ( ) ) = 85 0.7 0.3 E1 60.52 = GPa
F E f f = V 1 f F E c 85 F f 0.7 ( 0.9831 = ) = c 60.52 F
FIGURE 3.6 Longitudinal Young s modulus as function of fiber volume fraction and comparison with experimental data points for a typical glass/polyester lamina.
c h c tm/2 tf tm/2 tc FIGURE 3.7 A transverse stress applied to a representative volume element used to calculate transverse Young s modulus of a unidirectional lamina.
c = f = t = c , c = c , m c c E 2 ?= ?+ ? f and , t = and , = f f f f E f m t = m = m c m m E m h c ???? ??+ ???? ???? ?2= tm/2 tf tm/2 ?? tc
?? ??+ ?? ?? ?2= ?? 1 1 1 t t f m , = 2 + c and t t E E E f m c 1 V V f m = 2 + f E E E m
Example 3.4 Find the transverse Young's modulus of a Glass/Epoxy lamina with a fiber volume fraction of 70%. Use the properties of glass and epoxy from Tables 3.1 and 3.2, respectively. E f = 85 GPa 1 V V f m = 2 + f E E E Em = 3.4 GPa m 1 0.7 0.3 = 2 + 85 3.4 E = 2 10.37 GPa E
FIGURE 3.8 Transverse Young s modulus as a function of fiber volume fraction for constant fiber to matrix moduli ratio.
FIGURE 3.10 Theoretical values of transverse Youngs modulus as a function of fiber volume fraction for a boron/epoxy unidirectional lamina (Ef = 414 GPa, vf = 0.2, Em = 4.14 GPa, vm = 0.35) and comparison with experimental values. Figure (b) zooms figure (a) for fiber volume fraction between 0.45 and 0.75. (Experimental data from Hashin, Z., NASA tech. rep. contract no. NAS1-8818, November 1970.)
h h 1 1 1 1 tm/2 tm/2 tf tf tm/2 tm/2 (a) (a) tc tc tm/2 tm/2 tc tc T T tc + c tc + c tf tf T T tf + f tf + f tm/2 tm/2 Lc Lc (b) (b) FIGURE 3.11 A longitudinal stress applied to a representative volume element to calculate Poisson s ratio of unidirectional lamina.
T c T f T m = + T f T , = f t f T m T and , = m t m T c T = c t c T c T f T m t t = t + c f m
T f - = f , L f T m and , - = m L m T c - = 12 L c T c T f T m t t = t + c f m L c L f L m t - t - = t - m c 12 f f m
L c L f L m t - t - = t - m c 12 f f m L c = L f L m then , : = If h h 1 1 1 1 tm/2 tm/2 tf tf c t t = f t + m t tm/2 tm/2 12 f m (a) (a) tc tc t f m = 12 + c tm/2 tm/2 f m t t tc tc T T tc + c tc + c tf tf T T tf + f tf + f c tm/2 tm/2 = 12 V f + V m Lc Lc m f (b) (b)
Find the major and minor Poisson's ratio of a Glass/Epoxy lamina with a 70% fiber volume fraction. Use the properties of glass and epoxy from Tables 3.1 and 3.2, respectively. = f 0.2 = m 0.3 = 12 V f + V m m f 0.2 ( ( ) + ) 0.3 ( ( ) ) = 12 0.7 0.3 = 0.230
E1 = 60.52 GPa E2 = 10.37 GPa E 2 = 21 12 E 1 10.37 = 0.230 60.52 0.03941 =
h c c tm/2 tf tm/2 tc FIGURE 3.12 An in-plane shear stress applied to a representative volume element for finding in-plane shear modulus of a unidirectional lamina.
c = f + m = c t c , c and , = t f f f m = m t m
c = f + m c = c , = c t c , G c 12 f and , = f and , = t f f G f f = m m m = m t m G m f c m = t c 12 t f + f t m G G G m
f c m = t c 12 t f + f t m G G G m then , : c = f = If m 1 1 1 t t f m = 12 + c G G t G t f m c 1 V V f m = 12 + f G G G m
Find the in-plane shear modulus of a Glass/Epoxy lamina with a 70% fiber volume fraction. Use properties of glass and epoxy from Tables 3.1 and 3.2, respectively. GPa 85 = E f 0.2 = f = = m 3.4 0.3 GPa Em E f E = f G m = m G + 1 ( ) 2 + 1 ( ) 2 f m 3.40 85 = = + 1 ( ) 2 0.3 + 1 ( ) 2 0.2 = 1.308 GPa = 35.42 GPa
1 V V f m = 12 + f G G G m 1 0.70 0.30 = 12 + 35.42 1.308 G = 12 4.014 GPa G
FIGURE 3.13 Theoretical values of in-plane shear modulus as a function of fiber volume fraction and comparison with experimental values for a unidirectional glass/epoxy lamina (Gf = 30.19 GPa, Gm = 1.83 GPa). Figure (b) zooms figure (a) for fiber volume fraction between 0.45 and 0.75. (Experimental data from Hashin, Z., NASA tech. rep. contract no. NAS1-8818, November 1970.)
= 12 V f + V m m f 1 V V f m = 12 + f G G G m
Same as MOM equations for E1 and 12 but NOT for E2 and G12 E = 1 = 12 V f V f E + f + V m V m E m m f
( - ) E / f 1 + 1 V E E m f 2 = = m ( + ) - 1 V E / f E E f m The term is called the reinforcing factor and depends on the following Fiber Geometry Packing Geometry Loading Conditions Example: For a fiber geometry of circular fibers in a packing geometry of a square array, = 2
+ 1 V E f 2 = m - 1 V E f ( - ) E / f 1 E m = ( + ) E / f E m Ef/Em = 1 implies = 0, (homogeneous medium) - = implies = 1, (rigid inclusions) 1 Ef/Em implies (voids) Ef/Em 0
2 2 a b The term is depends on Fiber Geometry Packing Geometry Loading Conditions For a rectangular fiber cross-section of length a and width b in a hexagonal array, ? = 2(a/b), where a is in the direction of loading.
Find the transverse Young's modulus for a Glass/Epoxy lamina with a 70% fiber volume fraction. Use the properties for glass and epoxy from Tables 3.1 and 3.2, respectively. Use Halpin-Tsai equations for a circular fiber in a square array packing geometry. 2 = Ef = 85 GPa Em = 3.4 GPa 0.8889 ( )( ) + 1 2 0.7 E 2 = (85/3.4) 1 (85/3.4) + 2 0.8889 ( )( ) 3.4 1 0.7 ? = = 0.8889 = 2 20.20 GPa E
FIGURE 3.15 Theoretical values of transverse Youngs modulus as a function of fiber volume fraction and comparison with experimental values for boron/epoxy unidirectional lamina (Ef = 414 GPa, f = 0.2, Em = 4.14 GPa, m = 0.35). Figure (b) zooms figure (a) for fiber volume fraction between 0.45 and 0.75. (Experimental data from Hashin, Z., NASA tech. rep. contract no. NAS1-8818, November 1970.)
+ 1 V G f 12 = m - 1 V G f G ( 1 - ) / f G m = G ( + ) / f G m The term is called the reinforcing factor and depends on the following Fiber Geometry Packing Geometry Loading Conditions Example: For a fiber geometry of circular fibers in a packing geometry of a square array, = 1
12 12 a b For a rectangular fiber cross-section of length a and width b in a hexagonal array, ? = 3ln(? ?), where ? is in the direction of loading The term is depends on Fiber Geometry Packing Geometry Loading Conditions
Using Halpin-Tsai equations, find the shear modulus of a Glass/Epoxy composite with a 70% fiber volume fraction. Use the properties of glass and epoxy from Tables 3.1 and 3.2, respectively. Assume the fibers are circular and are packed in a square array. = 1.308 GPa Gm 1 = = 35.42 GPa Gf ( 1 - ) ( 0.9288 ( ) ( ) ) 35.42/1.30 8 + 1 1 0.7 G 12 = = 0.9288 ( ( ) ) 1.308 1 0.7 ( 1 + ) 35.42/1.30 8 G = 12 6.169 GPa 0.9288 =
Theoretical values of in-plane shear modulus as a function of fiber volume fraction compared with experimental values for unidirectional glass/epoxy lamina (Gf = 30.19 GPa, Gm = 1.83 GPa). Figure (b) zooms figure (a) for fiber volume fraction between 0.45 and 0.75. (Experimental data from Hashin, Z., NASA tech. rep. contract No. NAS1-8818, November 1970.)