Minimum Spanning Tree Algorithms
Explore different algorithms such as Kruskal's, Prim's, and Boruvka's for finding minimum spanning trees in graphs. Learn how they select safe edges and construct optimal spanning trees efficiently.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
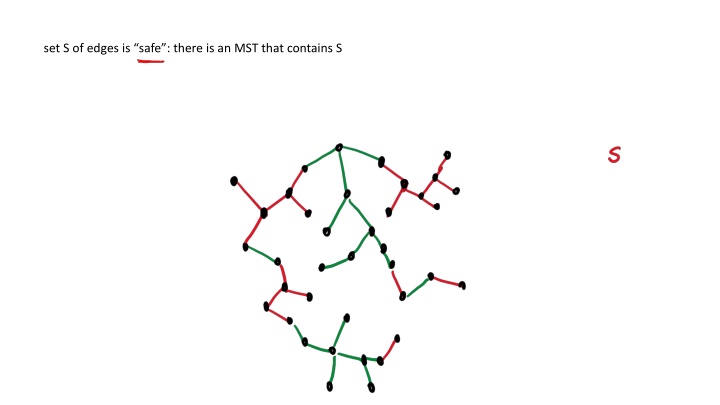
set S of edges is safe: there is an MST that contains S choose a component C in G[S] e min-weight edge crossing from C to its complement, then ? {?} is also safe
set S of edges is safe: there is an MST that contains S choose a component C in G[S] e min-weight edge crossing from C to its complement, then ? {?} is also safe Suppose not
set S of edges is safe: there is an MST that contains S choose a component C in G[S] e min-weight edge crossing from C to its complement, then ? {?} is also safe Suppose not
set S of edges is safe: there is an MST that contains S choose a component C in G[S] e min-weight edge crossing from C to its complement, then ? {?} is also safe Kruskal s algorithm: sort the edges in increasing order of weight Add an edge if it does not create a cycle with previously added edges, else reject it.
set S of edges is safe: there is an MST that contains S choose a component C in G[S] e min-weight edge crossing from C to its complement, then ? {?} is also safe Prim s algorithm: Start with a root node Each time chosen component = connected component of root node.
set S of edges is safe: there is an MST that contains S choose a component C in G[S] e min-weight edge crossing from C to its complement, then ? {?} is also safe Boruvka s algorithm: (assume distinct edge weights for simplicity) Each time, for each component choose the cheapest edge leaving it





















