Moments and Scalars in Physics

Chapter Four By Laith Batarseh Home Previous Next End

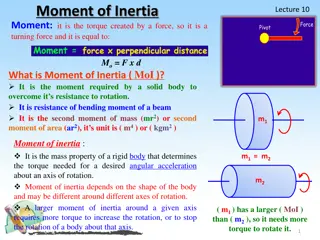
MOMENT SCALAR Definition Moment is defined as the tendency of a body lies under force to rotate about a point not on the line of the action of that force (i.e. there is a distance between the force and the rotation point ) Moment is a vector quantity Description Moment depends on two variables: The acting force Moment arm Home Previous Next End

MOMENT SCALAR Description Force Arm Tendency to rotate Home Previous Next End

MOMENT SCALAR Tendency for rotation Home Previous Next End

MOMENT SCALAR Magnitude F D Moment magnitude (M) = F.D Home Previous Next End

MOMENT SCALAR Direction Home Previous Next End

MOMENT SCALAR Solving procedures 1. Define the magnitudes of force (F) and arm (D) 2. Assume the positive direction (eg. Counter clock wise) 3. Find the magnitude of moment (M) as F.D 4. Give the moment the correct sign according to the tendency for rotation Home Previous Next End

MOMENT SCALAR Example [1] Find the moment caused by the following forces about point O 2m 2m O O 0.5m 0.5m 100 N 100 N (a) (b) Home Previous Next End

MOMENT SCALAR Example [1] Assume the CCW direction is the positive direction. 2m 2m O 0.5m O 0.5m 100 N 100 N (a) (b) Branch (a) Mo = F.d = -(100N)(0.5m) Mo=-50 N.m=50N.m CW Branch (b) Mo=F.d = (100N)(2m) Mo=200 N.m CCW + Home Previous Next + End

Principle Of Moments Principle of Moments some times called Vrigonon s theorem (Vrigonon is French mathematician 1654-1722). State that the moment of a force about a point equals the summation of the moments created by the force components In two dimensional problems: the magnitude is found as M = F.d and the direction is found by the right hand rule In three dimensional problems: the moment vector is found by M =rxf and the direction is determined by the vector notation (ie. i,j and k directions) Home Previous Next End

Principle Of Moments Example [1] Find the moment caused by the following forces about point O Home Previous Next End

Principle Of Moments Example [1] + Mo,1 = 100 sin(30) (10) = 500 N.m + Mo,2 =- 100 cos(30) (5) =- 433N.m M = Mo,1+Mo,2=500-433=67N CCW Home Previous Next End

Principle Of Moments Example [2] 1. Force analysis 100 cos(40) 120 sin(60) 1.2 m 100 sin(40) 120 cos(60) 0.3 m 2. Moment calculations + M = (100 cos(40))(1.5) ( 120 cos(60))(1.2) =43 N.m CCW Home Previous Next End

MOMENT SCALAR Moment resultant F1 d1 M1 O M2 d2 d3 M3 F3 F2 Mo = Mo = M1 + M2 M3 = F1d1+F2d2 F3d3 + Home Previous Next End

MOMENT SCALAR Example [2] Find the moment caused by the following forces about point O 100 N 2m 50 N O 75 N 1m 30o 3m 60 N 5m Home Previous Next End

MOMENT SCALAR Example [2] 100 N 2m 50 N O 75 N 1m 30o 3m 60 N 5m ( )( ) ( )( ) ( )( ) ( 3 60 2 = )( ) ( 5 )( ) 1 = + + 100 50 0 75 sin( 30 ) 75 cos( 30 ) M + o = 272 45 . m . 272 . 45 m . CW M N N o Home Previous Next End

MOMENT SCALAR Exercise Find the moment caused by the following forces about point O 100 N 5m 30o O 0.3m 45o 2m 300 N Home Previous Next End

MOMENT SCALAR Exercise 100sin (30)N 100 N 5m O 100cos (30)N 0.3m 300 cos (45)N 2m 300 sin (45)N 300 N ( )( ) ( 2 )( ) ( )( ) 5 = + 100 sin( 30 ) 300 cos( 45 ) 3 . 0 300 sin( 45 ) M + o = = 897 m . 897 m . CW M N N o Home Previous Next End

MOMENT VECTOR Cross product Cross product is a mathematical operation can be done on vectors Cross product for one time is done for two vectors The cross product of two vectors is a vector perpendicular to the plane of A and B The notation of vector A cross vector B is: C = AxB where C is the resultant vector from the cross product the vector C can be represented as : C =CUc where Uc is a unit vector in a direction perpendicular to the plane that contains both A and B. The value of the scalar quantity Cis given as : C=A.B.sin( ) where is the angle between A and B. Home Previous The cross product is controlled by the right-hand rule Next End

MOMENT VECTOR Graphical representation Uc Home Previous Next End

MOMENT VECTOR Cartesian vector formulation z K=ixj j=kxi y i=jxk Home x Previous Next End

MOMENT VECTOR Cartesian vector formulation A = Axi + Ayj + Azk B = Bxi + Byj + Bzk AxB=(AyBz -Az By)i-(Ax Bz - AzBx)j + (Ax By - AyBx)k i j k x = B A A A A x y z Home B B B Previous x y z Next End

MOMENT VECTOR Moment vector formulation M Mo = rxF d x Magnitude: Mo = rFsin( ) = Fd O r y Direction: perpendicular to x-y plane (z-direction) F i j k Best for three dimensional problems = x = F r Mo r r r Matrix notation: x y z F F F x y z Home Resultant moment:MRo= (rxF) Previous Next End

MOMENT VECTOR Example [1] Find the moment caused by the following forces about point O z F = [5i + 10j + 6k]N O y 3m 1m 2m Home x Previous Next End

MOMENT VECTOR Example [1] 1. Formulate the position vector (r) : r = 3i+2j+1k 2. Find the moment vector (Mo) by matrix notation i 3 j k 1 = = = + Mo r F 2 2 13 20 x i j k 5 10 6 r = 3i+2j+1k F = [5i + 10j + 6k]N Home Previous Next End

MOMENT VECTOR Example [2] Find the moment caused by the following forces about point O z O y x F = [-5i + 5j -5k]N Home Previous Next End

MOMENT VECTOR Example [2] 1. Formulate the position vector (r) : r= 15i + 10j +6k 2. Find the moment vector (Mo) by matrix notation i j k 6 = = = + + Mo r F 15 10 80 45 125 x i j k 5 5 5 Home Previous Next End

MOMENT VECTOR Summary Moment is a vector can be found by cross product and matrix notation Matrix notation: i j k = = Mo r F x r r r x y z F F F x y z Home Previous Next End

Principle Of Moments Principle of Moments some times called Vrigonon s theorem (Vrigonon is French mathematician 1654-1722). State that the moment of a force about a point equals the summation of the moments created by the force components In two dimensional problems: the magnitude is found as M = F.d and the direction is found by the right hand rule In three dimensional problems: the moment vector is found by M =rxf and the direction is determined by the vector notation (ie. i,j and k directions) Home Previous Next End

Principle Of Moments Example [1] Find the moment caused by the following forces about point O Home Previous Next End

Principle Of Moments Example [1] + Mo,1 = 100 sin(30) (10) = 500 N.m + Mo,2 =- 100 cos(30) (5) =- 433N.m M = Mo,1+Mo,2=500-433=67N CCW Home Previous Next End

Principle Of Moments Example [2] The following is a gate. In which direction this gate will rotate? 100N 40o 1.2 m 60o 0.3 m 120N Home Previous Next End

Principle Of Moments Example [2] 1. Force analysis 100 cos(40) 120 sin(60) 1.2 m 100 sin(40) 120 cos(60) 0.3 m 2. Moment calculations + M = (100 cos(40))(1.5) ( 120 cos(60))(1.2) =43 N.m CCW Home Previous Next End

Principle Of Moments Example [3] Find the moment caused by the following forces about point O Home Previous Next End

Principle Of Moments Example [2] i j k 6 = = = + Mo,1 r F 15 10 30 75 x i k r1= 15i + 10j +6k F1 = [5j]N 0 5 0 i j k = = = Mo,2 r F 15 10 6 30 75 r2= 15i + 10j -6k F2 = [-5j]N x i k 0 5 0 = M 60 i Home o Previous Next End

Moment of force about axis In many real cases, the force tendency to rotate is about a specified axis. Example : Moment components: Mo,1 = (100)(10) (about y-axis) Mo,2 = (100)(15) (about x-axis) Mo,3 =0 (about z-axis) Home Previous Next End

Moment of force about axis Magnitude Scalar analysis: M = F.d Vector analysis: u u u x , a r y , a r z , a r ( ) = = ua r F M . x a x y z F F F x y z Where: ua is a unit vector defining the direction of a-axis and given as ua = ua,xi + ua,yj + ua,zk Home To find the moment vector (Ma): Ma. ua Previous Next End

Moment of force about axis Example [1] + Mo,1 = 100 sin(30) (10) = 500 N.m + Mo,2 =- 100 cos(30) (5) =- 433N.m M = Mo,1+Mo,2=500-433=67N CCW Home Previous Next End

Moment of force about axis Example [2] Determine the magnitude of the moments of the force F about the x, y, and z axes. Solve the problem using a Cartesian vector approach using a scalar approach. Home Previous Next End

Moment of force about axis Example [2] using a Cartesian vector approach rAB = {5i + 4j -3k} m For the axes: x, y and z the unit vectors are i, j and k respectively. Mx = i . (rAB x F) My = j . (rAB x F) Mz = k . (rAB x F) 0 1 0 0 0 1 1 0 0 = = = = My 5 4 3 5 N m . Mz 5 4 3 30 N m . = = Mx 5 4 3 14 N m . Home 5 10 4 5 10 4 5 10 4 Previous Next End

Moment of force about axis Example [2] using a scalar approach Mx= Mx = 10(3) 4(4) = 14 N.m My= My = -5(3) + 4(5) = 5 N.m Mz= Mz = -5(4) + 10(5) = 30N.m Home Previous Next End

Moment of couple Definition Couple is the moment generated by two forces has the same magnitude and opposite direction. F d -F Home Previous Next End

Moment of couple Scalar analysis This analysis is considered for 2-D M problems The magnitude of moment is found by: M=F.d where F is the force F d magnitude. -F the direction of couple moment is perpendicular to the plain that contain the F and d and it is found by Home the right hand rule. Previous Next End

Moment of couple Example on scalar analysis F1 d1 F2 M1 = F1 . d1 M2 = F2 . d2 d2 -F2 -F1 Home Previous Next End

Moment of couple Vector analysis Derivation: M = rBx F + rAx F = (rB - rA) x F But: (rB - rA) = r Then: M = rx F This analysis is considered for 3-D problems The moment vector is found by: M=F x rwhere r is the position vector B directed between the forces F and F r -F Note that the moment vector is F dependent on the position vector A directed between the forces F and F rB (r). rA Home Previous O Next End

Moment of couple Example [1] Find the resultant moment couple produced by the following forces. All dimensions in m Home Previous Next End

Moment of couple Example [1] Solution: 1. By traditional moment analysis Mo = -(150)(7)-(150)(7) (200)(9)-(200)(9) = -5700 N.m + 2.By cpouple moment analysis + Mc = -(150)(14) (200)(18) = -5700 N.m Home Previous Next End

Moment of couple Example [2] Find the moment couple produced by the following force. All dimensions in m Home Previous Next End

Moment of couple Example [2] 1. F = 150 j 2. r = 3k 3. M = r x F = 150 j x 3k = {450N.m} i Home Previous M Next End

Moment of couple Equivalent couples in many of life applications, an equivalent couple is required to solve some technical problems such as space and size. Equivalent couples are the couples that have the same magnitude and same direction As you can see, the relation between the forces and the arm distances in equivalent coupels is reverse (for example, as we reduce the moment arm, the required force for equivalent couple increases) F1 F1.d1 = F2.d2 F2 = d2 d1 Home -F2 Previous Next -F1 End