Multiplication and Division Problem-Solving Strategies
In this educational material presented by Nick Meyer and Kathy Jones, District Elementary Math Coaches, various problem-solving strategies related to multiplication and division are explored. The content covers structuring problems, unknown group sizes, unknown numbers of groups, equal groups, arrays, and comparisons. It provides visual examples and exercises to enhance understanding of these mathematical concepts.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
MULTIPLICATION AND DIVISION PROBLEM SOLVING Nick Meyer and Kathy Jones, District Elementary Math Coaches October 26, 2017
Overview 3 1 2 3 4
Multiplication and Division 4 Review the problem-solving cards. Sort the cards by the type of problem they represent. Arrange them according to the grid on the next slide.
Multiplication and Division Structure 5 Size of Group Unknown (How many in each group?) Number of Groups Unknown (How many groups?) Unknown Product Equal Groups Area/Arrays Compare
Multiplication and Division Structure 6 Size of Group Unknown (How many in each group?) Number of Groups Unknown(How many groups?) Unknown Product Equal Groups There are A bags with B plums in each bag. How many plums are there in all? Area/Arrays If C plums are shared equally into B bags, then how many plums will be in each bag? If C plums are to be packed B to a bag, then how many bags are needed? Compare
Multiplication and Division Structure 7 Size of Group Unknown (How many in each group?) Number of Groups Unknown(How many groups?) Unknown Product Equal Groups There are A bags with B plums in each bag. How many plums are there in all? If C plums are shared equally into B bags, then how many plums will be in each bag? If C plums are to be packed B to a bag, then how many bags are needed? Area/ArraysThere are Arows of apples with B apples in each row. How many apples are there? If C apples are arranged into equal rows of B apples, how many rows will there be? If C apples are arranged into A equal rows, how many apples will be in each row? Compare
Multiplication and Division Structure 8 Size of Group Unknown (How many in each group?) Number of Groups Unknown (How many groups?) Unknown Product Equal Groups There are A bags with B plums in each bag. How many plums are there in all? If C plums are to be packed B to a bag, then how many bags are needed? If C plums are shared equally into B bags, then how many plums will be in each bag? Area/Arrays There are Arows of apples with B apples in each row. How many apples are there? If C apples are arranged into equal rows of B apples, how many rows will there be? If C apples are arranged into A equal rows, how many apples will be in each row? Compare A blue hat costs $B. A red hat costs A times as much as the blue hat. How much does the red hat cost? A red hat costs $C and a blue hat costs $B. How many times as much does the red hat cost as the blue hat? A red hat costs $C and that is A times as much as a blue hat costs. How much does a blue hat cost?
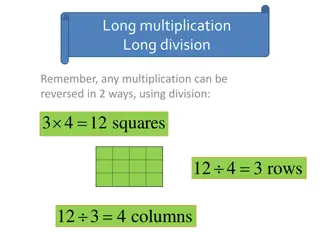
Structure 9 Number of Groups x Size of Group = Product N x S = P
Division 10 Read Problems A and B. (next slide) Make a math drawing for each problem. Write a number sentence. How are these problems similar and different?
Division 11 Problem B Problem A Rick puts 12 tennis balls equally into 3 cans. How many balls will be in each can? Rick puts 12 tennis balls into cans. Each can has 3 tennis balls. How many cans does Rick use?
Fact Strategies 13 Ms. Booker has 18 stickers in her sticker book. She puts 3 stickers on each page. How many pages will she use?
Fact Strategies 14 If I had 8 boxes of peaches with 6 peaches in each box, how many peaches would I have?
Fact Strategies 15 I have 6 bags of books with 7 books in each bag. How many books do I have?
23 x 8 17
23 x 18 18 2 3 x 1 8 1 8 4 + 2 3 0 4 1 4
Long Division 19 Bailey s Bakery donated 596 cupcakes to the school bake sale. They packaged them in groups of 4. How many packages of cupcakes did they donate?
Much larger numbers 20 Michael has a collection of 1,404 sports cards. He hopes to sell the collection in packs of 36 cards and make $633.75 when all the packs are sold. If each pack is priced the same, how much should Michael charge per pack?
Much smaller numbers 21 Joanne has 2 oranges. She wants to give 1/3 of an orange to each of her friends on the soccer team. How many of her friends can get 1/3 of an orange? How much of an orange will Joanne have left over?
How can you help? 22 Ask your student about his/her math drawing. Where does each quantity appear? Ask your student about his/her method for multiplying and dividing. How do they decide to break the numbers into manageable parts?