Multiplication Grid Practice and Expansion Exercises

Practice and expand multiplication grids, simplify expressions, and learn to expand brackets using various methods. Master the FOIL method, grid method, and basic algebraic manipulations. Improve your mathematical skills with these structured exercises.

• Multiplication grid
• Expansion exercises
• Algebraic manipulation
• FOIL method
• Grid method

edv_c Follow

Uploaded on Feb 26, 2025 | 2 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

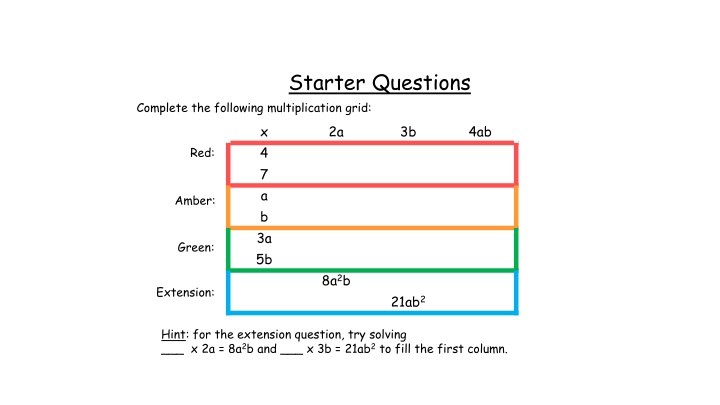
1. Starter Questions Complete the following multiplication grid: x 4 7 a b 3a 5b 2a 3b 4ab Red: Amber: Green: 8a2b Extension: 21ab2 Hint: for the extension question, try solving ___ x 2a = 8a2b and ___ x 3b = 21ab2 to fill the first column.

2. Answers x 4 7 a b 3a 5b 4ab 7ab 2a 8a 14a 2a2 2ab 6a2 10ab 8a2b 14a2b 3b 12b 21b 3ab 3b2 9ab 15b2 12ab2 21ab2 4ab 16ab 28ab 4a2b 4ab2 12a2b 20ab2 16a2b2 28a2b2

3. Everything outside the brackets must multiply everything inside the brackets. Expand 4 (3y + 7) = 12y + 28 Expand 3x (2y - 1) = 6xy - 3x

4. Answers 2a 6 3b + 15 2c 2 3d + 3 10e 20 8 12f g + 4g h - 3h 2k + 5k 3mn 2m 2pq + 12p 6r 6rs

5. Expand and simplify: a(b - a) + a(a + 2) = ab - a + a + 2a = ab + 2a m(m 2n) + 3m(5n + 3m) = m - 2mn + 15mn + 9m = 10m + 13mn

6. Answers 24x 18 + 12x 3 = 36x 21 25z + 60 + 15z 6 = 40z + 54 5y + 6y + y + 5y = 6y + 11y 5r + pr + 2r + 2pr = 7r + 3pr 4st + 2ps + 2st + 2pt = 6st + 2ps + 2pt 12ab + 4ap + 2a + 2ap = 12ab + 6ap + 2a

7. Starter Expand and simplify (where possible): = 6a + 6b 6 (a + b) = x + xy x (x + y) = 7m + 5n 4 (m + 2n) + 3 (m n) = -x + 9xy 2x (x + 3y) 3x (x y)

8. (p + 3)(p 7) There are two different methods we can use to expand these brackets.

9. Grid Method (p + 3)(p 7) x p p +3 +3p -21 p -7p -7 p - 7p + 3p - 21 p - 4p - 21

10. FOIL Method (p + 3)(p 7) First: Outside: Inside: Last: p -7p +3p -21 p - 7p + 3p - 21 p - 4p - 21

11. Questions 1. (x + 4)(x + 2) 4. (x + 8)(x + 11) 2. (x + 7)(x + 8) 5. (x + 5)(x + 7) 3. (x + 3)(x + 2) 6. (x + 4)(x + 4) 1. (x + 4)(x - 2) 4. (x - 8)(x - 11) 2. (x - 7)(x + 8) 5. (x - 5)(x + 7) 3. (x - 3)(x + 2) 6. (x - 4)(x - 4) 1. (x + 4)(x - 4) 4. (x + 8) 2. (x + 3)(x - 3) 5. (x - 5) 3. (x + 3) 6. (x - 7)

12. Answers 1. x + 6x + 8 4. x + 19x + 88 2. x + 15x + 56 5. x + 12x + 35 3. x + 5x + 6 6. x + 8x + 16 1. x + 2x - 8 4. x - 19x + 88 2. x + x - 56 5. x + 2x - 35 3. x - x - 6 6. x - 8x + 16 1. x - 16 4. x + 16x + 64 2. x - 9 5. x - 10x + 25 3. x + 6x +9 6. x - 14x + 49

13. (4y - 3)(2y 5) What is different about this example?

14. Grid Method (4y - 3)(2y 5) x 2y -5 4y 8y -20y -3 -6y +15 8y - 20y - 6y + 15 8y - 26p + 15

15. FOIL Method (4y - 3)(2y 5) First: Outside: Inside: Last: 8y -20y -6y +15 8y - 20y - 6y + 15 8y - 26p + 15

16. Questions 1. (2x + 4)(x + 2) 4. (x + 8)(3x + 11) 5. (2x + 5)(3x + 7) 6. (4x + 4)(3x + 4) 2. (x + 7)(3x + 8) 3. (5x + 3)(x + 2) 1. (2x + 4)(3x - 2) 2. (4x - 7)(2x + 8) 3. (x - 3)(7x + 2) 4. (3x - 8)(4x - 11) 5. (6x - 5)(2x + 7) 6. (3x - 4)(5x - 4) 1. (2x + 4)(2x - 4) 2. (3x + 3)(3x - 3) 3. (6x + 3) 4. (5x + 8) 5. (4x - 5) 6. (11x - 7)

17. Answers 1. 2x + 8x + 8 4. 3x + 35x + 88 5. 6x + 29x + 35 6. 12x + 28x + 16 2. 3x + 29x + 56 3. 5x + 13x + 6 1. 6x + 8x 8 4. 12x - 57x + 88 5. 12x + 20x 33 6. 15x - 32x + 16 2. 8x + 10x 56 3. 7x - 19x 6 1. 4x - 16 4. 25x + 80x + 64 5. 16x - 40x + 25 6. 121x - 154x + 49 2. 9x - 9 3. 36x + 36x + 9

18. Sketching Graphs (x + 3)(x 7) = x - 4x - 21 x tells us the shape of the graph -21 tells us the y-intercept y -21

19. Sketching Graphs (x + 3)(x 7) = 0 (x + 3) = 0 So x = -3 (x - 7) = 0 So x = 7 These are the x-intercepts

20. Sketching Graphs y = (x + 3)(x 7) y y-intercept = -21 x-intercepts = -3, 7 Sketch the graphs for the equations you have just expanded. x 7 -3 -21

21. Starter a) Where do these graphs cross the x-axis? b)Expand the brackets c) Where do these graphs cross the y-axis? 1. y = (x 4)(x + 2) 2. y = (x 7)(x 3) 3. y = (x + 5)

22. a) Where do these graphs cross the x-axis? b) Expand the brackets c) Where do these graphs cross the y-axis? 1. y = (x 4)(x + 2) x = 4 or -2 y = x - 2x - 8 y-intercept at -8

23. a) Where do these graphs cross the x-axis? b) Expand the brackets c) Where do these graphs cross the y-axis? 2. y = (x 7)(x - 3) x = 7 or 3 y = x - 10x + 21 y-intercept at +21

24. a) Where do these graphs cross the x-axis? b) Expand the brackets c) Where do these graphs cross the y-axis? 3. y = (x + 5) x = -5 y = x + 10x + 25 y-intercept at +25

25. If the greatest power of x is 1, the equation is linear. Eg: y = 4x - 1 If the greatest power of x is 2 (x ), the equation is quadratic. Eg: y = x + 6x 2 If the greatest power of x is 3 (x ), the equation is cubic. Eg: y = x - 5x + 4x - 9

26. True or False: y = 3x + 6x 2 is a cubic equation y = 2x - 9x is a cubic equation y = 5 3x is a linear equation y = 3 7x is a quadratic equation

27. Show me: A linear equation where x = 2 and y = 7 A quadratic equation where x = 2 and y = 7 A cubic equation where x = 2 and y = 7

28. Where does the graph y = (x + 4)(x + 1)(x 2) cross the x-axis and the y-axis? If (x + 4)(x + 1)(x 2) = 0, x = -4, -1 or 2 To find where the graph crosses the y-axis, we ll need to expand the brackets Remember the solutions of x are where the graph crosses the x-axis!

29. (x + 4)(x + 1)(x 2) Start by expanding one pair of brackets. x x x x +1 +x -2 -2x -2 = x - 2x + x - 2 = x - x - 2 So (x + 4)(x + 1)(x 2) = (x + 4)(x - x 2)

30. (x + 4)(x + 1)(x 2) = (x + 4)(x - x 2) Now we can expand the rest. x x x x -x -x -4x -2 -2x +4 -8 +4x = x + 4x - x - 4x 2x - 8 = x + 3x - 6x - 8 So (x + 4)(x + 1)(x 2) = x + 3x - 6x - 8

31. Where does the graph y = (x + 4)(x + 1)(x 2) cross the x-axis and the y-axis? If (x + 4)(x + 1)(x 2) = 0, x = -4, -1 or 2 (x + 4)(x + 1)(x 2) = x + 3x - 6x - 8 The y-intercept is -8.

32. Where does the graph y = (2x - 1)(x + 3)(x + 5) cross the x-axis and the y-axis? If (2x - 1)(x + 3)(x + 5) = 0, x = , -3 or -5 Start by expanding one pair of brackets. So (2x - 1)(x + 3)(x + 5) = (2x - 1)(x + 8x + 15) Now we can expand the rest. So (2x - 1)(x + 3)(x + 5) = 2x + 15x + 22x - 15 The y-intercept is -15.

33. Where does the graph y = 5x(2x - 3)(x - 2) cross the x-axis and the y-axis? If 5x(2x - 3)(x - 2) = 0, x = 0, 3/2 or 2 Start by expanding one pair of brackets. So 5x(2x - 3)(x - 2) = 5x(2x - 7x + 6) Now we can expand the rest. So 5x(2x - 3)(x - 2) = 10x - 35x + 30x The y-intercept is 0.

34. Answers 1. y = 6x + 3x 2 y = 12 11x 2. Use the solutions of the following equations to match them to their corresponding graphs below. y = (x + 3)(x 1)(x 4) y = (x 2)(x + 1)(x + 3) Which of the following equations are cubic? (Circle them ) y = 8x4 + 10x - 7 y = 2x - 5x + 1 y = 5x + 6 y = 4x + 2x + 9 y = x - 7x + 8x 18 y = x - 16 y = 5x(x + 1)(2x 1)

35. Answers 3. Expand the following expressions. a. (x + 2)(x + 5)(x + 1) = x + 8x + 17x + 10 b. (x 3)(x + 4)(x 2) = x - x - 14x + 24 c. x(x + 5)(x 4) = x + x - 20x d. (x + 3) = x + 9x + 27x + 27 4. What equations do these graphs represent? y = (x + 3)(x + 1)(x 1), y = (x + 1)(x 1)(x 2), y = (x + 1)(x 2)(x 3) 5. How many solutions does each cubic equation have? a. 3 c. 3 e. 3 b. d. f. 1 2 3