Neural Networks: Fundamentals, Models, and Equations
Explore the world of neural networks by delving into topics such as assignment due dates, decision boundaries, Gaussian generative models, activation functions, and loss functions. Learn about the optimization process, single neuron systems, multilayer perceptrons, and neural network equations in this comprehensive overview facilitated by Instructor Pat Virtue.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
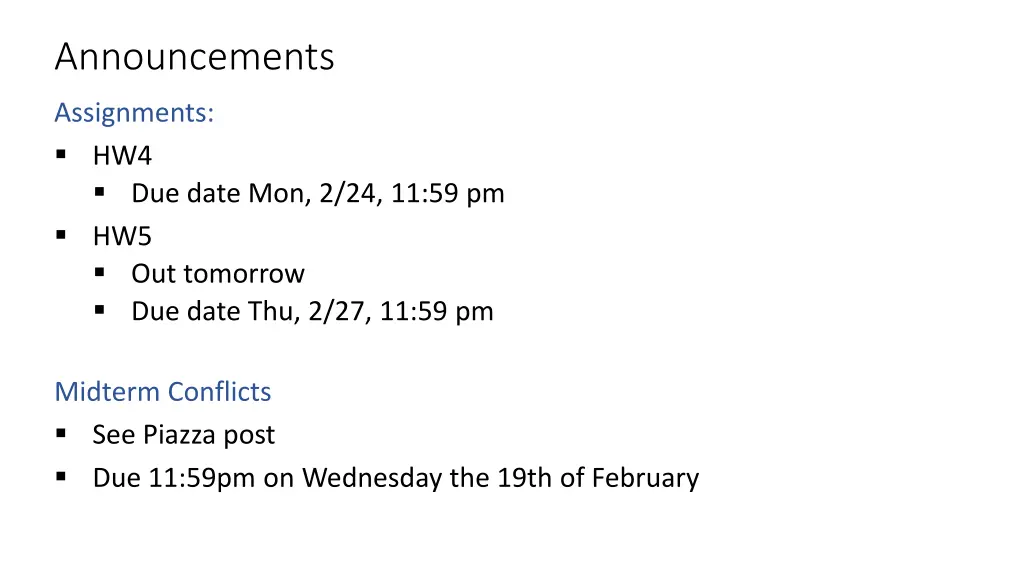
Announcements Assignments: HW4 Due date Mon, 2/24, 11:59 pm HW5 Out tomorrow Due date Thu, 2/27, 11:59 pm Midterm Conflicts See Piazza post Due 11:59pm on Wednesday the 19th of February
Plan Last time Decision Boundaries Gaussian Generative Models Neural Networks Today Neural Networks Universal Approximation Optimization / Backpropagation (Convolutional Neural Networks)
Introduction to Machine Learning Neural Networks Instructor: Pat Virtue
Single Neuron Single neuron system Perceptron (if ? is step function) Logistic regression (if ? is sigmoid) ?1 ?1 Computed Value ?1 True Label ? ? ?2 ?? = ?1 ?2 ?? = ? ???? ?
Optimizing How do we find the best set of weights? ?? = ? ???? ?
Activation Functions It would be really helpful to have a g(z) that was nicely differentiable Hard threshold: ? ? = 1 ? 0 ?? ??= 0 ? 0 0 ? < 0 0 ? < 0 1 ?? ??= ? ? 1 ? ? Sigmoid: (Softmax) ? ? = 1+? ? ?? ??= 1 ? 0 0 ? < 0 ReLU: ? ? = ???(0,?)
Loss Functions Regression 2= ??? 2 MSE (SSE): ?, ? = ? ?2 ?? Classification Cross entropy: ?, ? = ? ??log ??
Multilayer Perceptrons A multilayer perceptron is a feedforward neural network with at least one hidden layer (nodes that are neither inputs nor outputs) MLPs with enough hidden nodes can represent any function Slide from UC Berkeley AI
Neural Network Equations ?21 ?11 ?111 ?112 ? ?1 ?211 ?31 ?113 ?212 ? ?311 ?221 ?121 ?41 ?12 ?22 ? ?2 ? ?123 ?32 ?221 ?321 ? ?131 ?13 ?23 ?232 ? ?3 w133 ?? = ?4,1 ?1,1= ?1 ?4,1= ? ??3,?,1 ?3,? ?? = ? ?3,?,1 ? ?2,?,? ? ?1,?,? ?? ?3,1= ? ??2,?,1 ?2,? ? ? ? ??,1= ? ??? 1,?,1 ?? 1,?
Optimizing How do we find the best set of weights? ?? = ? ?3,?,1 ? ?2,?,? ? ?1,?,? ?? ? ? ?
Neural Network Equations ?21 ?11 ?111 ?112 ? ?1 ?211 ?31 ?113 ?212 ? ?311 ?221 ?121 ?41 ?12 ?22 ? ?2 ? ?123 ?32 ?221 ?321 ? ?131 ?13 ?23 ?232 ? ?3 w133 How would you represent this specific network in PyTorch?
Neural Networks Properties Practical considerations Large number of neurons Danger for overfitting Modelling assumptions vs data assumptions trade-off Gradient descent can easily get stuck local optima What if there are no non-linear activations? A deep neural network with only linear layers can be reduced to an exactly equivalent single linear layer Universal Approximation Theorem: A two-layer neural network with a sufficient number of neurons can approximate any continuous function to any desired accuracy.
Network to Approximate a 1-D Function Design a network to approximate this function using: Linear, Sigmoid, Step, or ReLU
Network to Approximate a 1-D Function Design a network to approximate this function using: Linear, Sigmoid, Step, or ReLU
Network to Approximate Binary Classification Approximate function ? ?1,?2 = ?1 ?2
Network to Approximate Binary Classification Approximate function ? ?1,?2 = ?1 ?2
Network to Approximate Binary Classification Approximate arbitrary decision boundary https://cs.stanford.edu/people/karpathy/convnetjs/demo/classify2d.html
Network to Approximate Binary Classification Approximate arbitrary decision boundary https://cs.stanford.edu/people/karpathy/convnetjs/demo/classify2d.html
Reminder: Calculus Chain Rule (scalar version) ? = ? ? ? = ? ? ?? ??=?? ?? ?? ??
Network Optimization ? ? = ?3 ?3= ?3(?3,?2) ?2= ?2?2,?1 ?1= ?1?1,?
Backpropagation (so-far) Compute derivatives per layer, utilizing previous derivatives Objective: ? ? Arbitrary layer: ? = ? ?,? Need: ?? ??= ?? ?? ?? ?? ?? ??= ?? ?? ?? ??