Optimal Path Finding

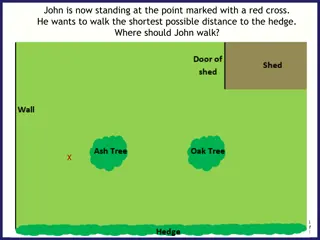
John is standing at the point marked with a red cross. He wants to walk so that he is always the same distance away from the hedge and the wall. Where should John walk? X

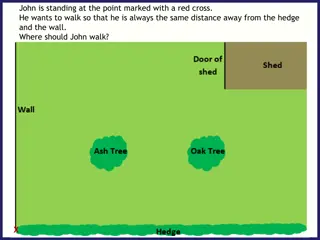
John is standing at the point marked with a red cross. He wants to walk so that he is always the same distance away from the hedge and the wall. How do you know he is exactly half way between the wall and the hedge? X

John is standing at the point marked with a cross. He wants to walk so that he is always the same distance away from the hedge and the wall. What would be the same if the path had been drawn perfectly? X

The ideal flight path for the plane to land is midway between the maximum and minimum angle of descent. What path should the plane take?

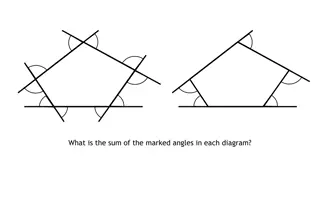
To draw the path accurately we can use a construction known as an angle bisector. What do you think the word bisector means? bisect: to split into two equal parts

When constructing an angle bisector every point on the path drawn is equidistant from one side as it is from the other. The angle has been perfectly cut in half.

Anchor compasses at the vertex of the angle (point Q) Draw a circle with radius less than QP and QR Label the points where the circle intersects QP and QR A and B respectively Do not alter the width of the compasses 7

Anchor compasses at point A Draw a circle with centre A Do not alter the width of the compasses 8

Anchor compasses at point B Draw a circle with centre B 9

Draw a line from Q to where the two circles with centres A and B intersect. Line QC bisects angle PQR 10

Why is QA is congruent to QB? Why does the line QC bisects the angle PQR? Reason: They were both drawn with the same compass width. Reason: AQC and BQC are adjacent and congruent. Why are angles AQC and BQC are congruent? Reason: Corresponding parts of congruent triangles are congruent. 11

Bisecting Angles Bisect an obtuse angle ABC

Anchor compasses at the vertex of the angle (point B) Draw a circle with radius less than BA and BC Label the points where the circle intersects BA and BC D and E respectively Do not alter the width of the compasses 13

Anchor compasses at point E Draw a circle with centre E Do not alter the width of the compasses 14

Anchor compasses at point D Draw a circle with centre D 15

Draw a line from B to where the two circles with centres D and E intersect. Line BG bisects angle ABC 16

In your books.. Q1. Sketch these angles and bisect them with compasses and a ruler

In your books Q2. Sketch these polygons and bisect angle ABC

In your books Q3. Using a protractor, draw an angle of 64 . Using a compass and ruler only, construct its angle bisector. Check your answer by measuring the two angles formed. Q4. Using a protractor, draw an angle of 120 . Using a compass and ruler only, construct its angle bisector. Check your answer by measuring the two angles formed. Q5. Draw a triangle and construct the angle bisector of each vertex. Draw the largest possible circle that does not exit the triangle.

Q5. Draw a triangle and construct the angle bisector of each corner You should find that the bisectors intersect at a single point inside the triangle! Now using the point of intersection as centre, draw the largest possible circle that does not leave the triangle You should find that the circle touches all three sides of the triangle This works with anytriangle Can you explain why this happens?!

Challenge Problem: Bisect all 4 angles using the fewest arcs and lines. (Record: 4 arcs, 2 lines)