Optimizing Dijkstra's Algorithm for Single-Source Shortest Path
Explore Dijkstra's Algorithm for Single-Source Shortest Path with non-negative edge weights, focusing on efficient distance calculations and edge relaxation. Discover step-by-step visualizations of the algorithm in action and learn how to apply it in real-world scenarios effectively.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
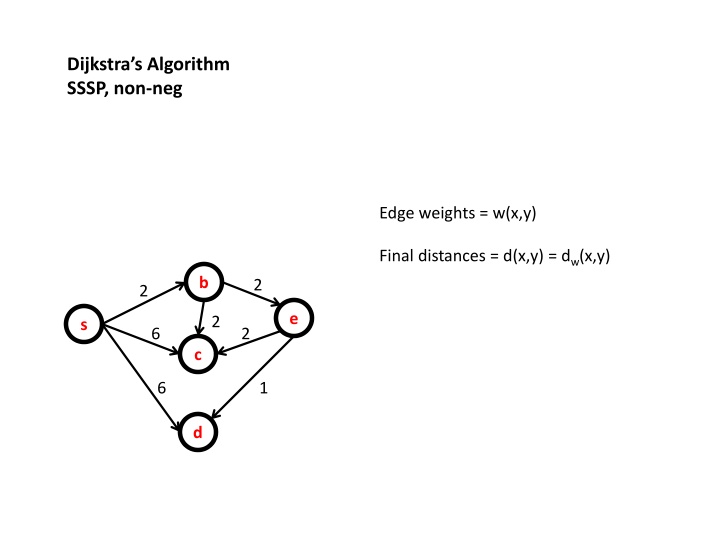
Dijkstras Algorithm SSSP, non-neg Edge weights = w(x,y) Final distances = d(x,y) = dw(x,y) b 2 2 e 2 s 6 2 c 6 1 d
Dijkstras Algorithm SSSP, non-neg s b c d e 0 L(x) b 2 2 e 2 s 6 2 x <- extractmin c 6 1 // L(x) is the distance of s to x // mark x as final d "relax all the edges out of x L(y) <- min ( L(y), L(x) + w(x,y) )
Dijkstras Algorithm SSSP, non-neg s b c d e 0 L(x) b 2 2 e 2 s 6 2 x <- extractmin c 6 1 // L(x) is the distance of s to x // mark x as final d "relax all the edges out of x L(y) <- min ( L(y), L(x) + w(x,y) )
Dijkstras Algorithm SSSP, non-neg s b c d e 0 2 6 6 L(x) b 2 2 e 2 s 6 2 x <- extractmin c 6 1 // L(x) is the distance of s to x // mark x as final d "relax all the edges out of x L(y) <- min ( L(y), L(x) + w(x,y) )
Dijkstras Algorithm SSSP, non-neg s b c d e 0 2 4 6 4 L(x) b 2 2 e 2 s 6 2 x <- extractmin c 6 1 // L(x) is the distance of s to x // mark x as final d "relax all the edges out of x L(y) <- min ( L(y), L(x) + w(x,y) )
Dijkstras Algorithm SSSP, non-neg s b c d e 0 2 4 6 4 L(x) b 2 2 e 2 s 6 2 x <- extractmin c 6 1 // L(x) is the distance of s to x // mark x as final d "relax all the edges out of x L(y) <- min ( L(y), L(x) + w(x,y) )
Dijkstras Algorithm SSSP, non-neg s b c d e 0 2 4 5 4 L(x) b 2 2 e 2 s 6 2 x <- extractmin c 6 1 // L(x) is the distance of s to x // mark x as final d "relax all the edges out of x L(y) <- min ( L(y), L(x) + w(x,y) )
Dijkstras Algorithm SSSP, non-neg makeheap m decrease-keys n extract-mins s b c d e 0 2 4 5 4 L(x) b 2 2 e 2 s 6 2 x <- extractmin c 6 1 // L(x) is the distance of s to x // mark x as final d "relax all the edges out of x L(y) <- min ( L(y), L(x) + w(x,y) )
Dijkstras Algorithm SSSP, non-neg 1. values in L array correspond to some path length, so never less than SP length 2. when x made final, L(x) = shortest path length
Dijkstras Algorithm SSSP, negative lengths? Change one edge length so that Dijkstra s algorithm gives wrong answer s b c d e 0 L(x) b 2 2 e 2 s 6 2 x <- extractmin c 6 1 // L(x) is the distance of s to x // mark x as final d "relax all the edges out of x L(y) <- min ( L(y), L(x) + w(x,y) )
Bellman-Ford-Moore Algorithm SSSP, neg wts OK!!
Bellman-Ford-Moore Algorithm SSSP, neg wts OK n rounds m time per round O(mn) time s b c d e 0 L(x) // L(x) is an upper bound on d(s,x) b 2 2 for t = 1 to n-1 for all vertices x e 2 s -2 6 c // "relax all the edges out of x L(y) <- min ( L(y), L(x) + w(x,y) ) 6 1 d Claim: if graph has non negative cycles, B-F-M is OK. Proof: induction. At end of round t, L(y) is shortest path using at most t edges.
Bellman-Ford-Moore Algorithm SSSP, neg wts OK n rounds m time per round O(mn) time s b c d e 0 2 2 5 4 L(x) // L(x) is an upper bound on d(s,x) b 2 2 for t = 1 to n-1 for all vertices x e 2 s -2 6 c // "relax all the edges out of x L(y) <- min ( L(y), L(x) + w(x,y) ) 6 1 d Claim: if graph has non negative cycles, B-F-M is OK. Proof: induction. At end of round t, L(y) is shortest path using at most t edges.
Bellman-Ford-Moore Algorithm SSSP, neg wts OK n rounds m time per round O(mn) time s b c d e 0 2 2 5 4 L(x) // L(x) is an upper bound on w(s,x) b 2 2 for t = 1 to n-1 for all vertices x e 2 s -2 6 c // "relax all the edges out of x L(y) <- min ( L(y), L(x) + w(x,y) ) 6 1 d Claim: If at end, some edge xy is over-tight ( it has L(y) > L(x) + w(x,y) ) then graph has negative cycle.