Otolaryngology - Sinonasal Tumours Classification and Staging
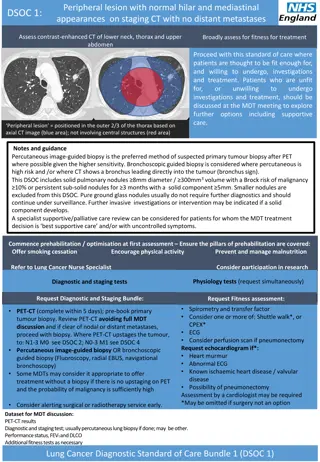
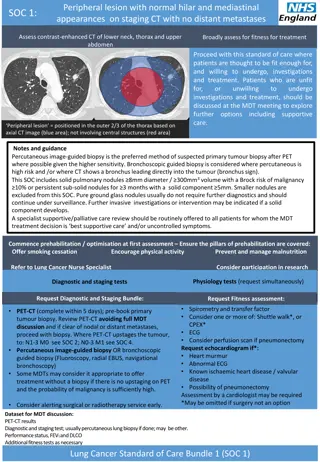
Otolaryngology in relation to sinonasal tumours involves classification into benign and malignant groups based on types like epithelial and non-epithelial tumors. The staging system for these tumors includes UICC classifications and criteria specific to maxillary and ethmoid sinuses. Clinical features such as nasal discharge, facial swelling, gum or palate ulcers, and pain are outlined. Visual aids illustrate the different stages and characteristics of sinonasal tumors.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Agenda Why choose our specification The GCSE reforms Changes to all GCSEs in Statistics Our new GCSE (9 1) qualification: Overview Content Assessment Support Contact details and next steps
The specification and sample assessment materials can be found here: http://quals.pearson.com/stats17
Statistics for the real world Straightforward assessment structure Content that develops transferable skills Clear and familiar course content and approach Question papers that support a range of abilities Support resources to help you plan, teach, track and assess
Why teach GCSE Statistics? The world is awash with data. It is estimated that 2.5 1018 bytes of data are created every day Economies increasingly are data dependent and use data-intensive technologies: government, finance, manufacturing, health, education, media, banking, retail, science, sports, The ability to make sense of data is an essential skill for working life and full citizenship in a modern society GCSE Statistics develops key transferable skills which students take into their other studies and their wider lives GCSE Statistics counts in a slot of the open element of Progress 8
Overview of the changes GCSE Statistics is changing for first teaching 2017 and first assessment 2019. The regulatory reforms impacting all GCSEs are: Fully linear structure Updated subject content (from the DfE) and assessment requirements (from Ofqual) General increase in level of demand and challenge, including extended response questions New 9 to 1 grading scale Tiering only in certain subjects (includes Statistics) Non-examination assessment permitted only where it is the only valid option No change to guided learning hours (120 glh)
The new 91 grading scale Broadly the same proportion of students will achieve grade 4 and above as currently achieve grade C and above Broadly the same proportion of students will achieve grade 7 and above as currently achieve grade A and above The bottom of grade 1 will be aligned to the bottom of grade G Strong pass Standard pass Source: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/465873 /your_qualification_our_regulation.pdf
The change timeline 2016 2017 2018 2019 Current specification Last 2-year course commences Last 1-year course commences Last assessment opportunity New specification First teaching of 2-year course First teaching of 1-year course First assessment opportunity The last available assessment for the current GCSE Statistics is summer 2018 The reformed GCSEs will be reported in the 2019 performance tables
Changes to all GCSEs in Statistics
Tiering Ofqual has approved the retention of tiering for GCSE Statistics. The approach to tiering follows that of GCSE (9 1) Mathematics Foundation tier: will span grades 1 to 5 (five grade range) students will be assessed on content in standard and underlined type papers will reach a higher level of demand than current papers Higher tier: will span grades 4 to 9 (six grade range) students will be assessed on all content papers will: start at a higher level of demand and reach a higher level of demand than current papers
Content changes Increased exam emphasis on knowledge related to data collection: planning an investigation, design constraints, populations and sampling, controlling variables, minimising distortion, cleaning data, acknowledging sources, etc. Expectation that students will use correct statistical terminology and notation including formal notation for probability Some new topics at each tier, especially at Higher tier Some additional formulae to be used, or learnt and used, at each tier Overlap with GCSE Mathematics reduced
Assessment changes New assessment objectives Controlled assessment has been removed. All new GCSEs in Statistics will be assessed entirely by written examination Understanding of the statistical enquiry cycle will be assessed in written form Target assessment objective weightings (with small ranges permissible)
Impact of the changes I There is some increase in the amount of content to cover at each tier, especially Higher: May have implications for teaching time and delivery models Removal of controlled assessment: Frees up curriculum time to cover the new content requirements Continuing to incorporate some practical work will support students with AO3 questions
Impact of the changes II Increase in demand of the assessment: Tier choice criteria may need to be reconsidered, especially for borderline students Inclusion of extended response questions: Strategies to support students including those with EAL and literacy needs Some increase in the number of formulae to be learnt: Strategies may be needed to support some students The increase in subject breadth and depth: Some non-specialist teachers may benefit from CPD
Our approach Our approach has been to develop a Statistics qualification that: you will know and recognise is clear about content coverage will support you in developing students statistical understanding and transferable skills To achieve this we have worked with the teaching community, higher education and statistics educationalists to design our new qualification We have gathered over 300 sets of views and had more than 80 conversations with statistics teachers and educationalists We have trialled our new questions with over 250 students.
Our design principles Straightforward assessment structure Two papers of equal size, length and weighting All content and AOs targeted equally in both papers Content that develops transferable skills Develops understanding of how to interpret and apply data Supports skills development for progression in a wide range of subjects including A Level Mathematics Clear and familiar course content and approach Clear content coverage with plenty of guidance Structure follows that of the current specification for ease of use Question papers that support a range of abilities Clear questions and presentation of data Careful ramping within questions, across papers and between tiers Engaging real-life statistical material and contexts Support resources to help you plan, teach, track and assess
Specification overview Available at Foundation tier and Higher tier Paper Content overview Summary of assessment Paper 1 (50%) 1 hour 30 mins 80 marks 1. The collection of data 2. Processing, representing and analysing data 3. Probability All assessment objectives targeted Paper 2 (50%) 1 hour 30 mins 80 marks 1. The collection of data 2. Processing, representing and analysing data 3. Probability All assessment objectives targeted
Content overview The specification content has been updated in line with the DfE subject content Our specification sets out Foundation and Higher tier content separately and we tell you where topics are not required at Foundation Organisation of content within each tier: follows that of the current specification reflects the sequence of the statistical enquiry cycle.
Statistical enquiry cycle Through using the SEC students need to: 1. Understand the importance of initial planning 2. Recognise the constraints in sourcing appropriate data 3. Understand ways that data can be processed and presented including through use of technology 4. Interpret results in context 5. Understand importance of clear and concise communication
Content changes Foundation Topics new to Foundation tier include: Context sensitivity as a source of bias Judgement, convenience and quota sampling RPI, CPI Rates of change over time e.g. birth rates Interpretation of Spearman s rank correlation coefficient Effect of sample size when estimating probability Venn diagrams Conditional probability
Content changes Higher I Topics new to Higher tier include: Misuse of frequency density formula Geometric mean Calculation of skewness Interdecile range Identify outliers using IQR or standard deviation Deeper understanding of Normal distribution
Content changes Higher II Topics new to Higher tier include (continued): Distribution of sample means Placement of action and warning lines No expansion formula given for binomial calculations Multivariate data Interpretation of Pearson s product moment correlation coefficient Distinction between Spearman s and Pearson s coefficients
Removed content Foundation Effects of accuracy on measurements Non-linear models Higher Effects of accuracy on measurements Non-linear models Discrete uniform distribution Simulation for more complex probabilities
Formulae There are statistics formulae that students: are expected to know should be able to use - these will be given in the assessment There are also GCSE Mathematics formulae that students are expected to know New in 2017 Foundation Higher Statistics formulae to be known: Mean Double mean point Probability formulae Mean, Geometric mean Interdecile range Outliers using SD Probability formulae Statistics formulae to be used: Rates of change Skew Rates of change
Examples of formulae Formulae students are expected to know include: Additional law for mutually exclusive events: P(A or B) = P(A) + P(B) Multiplication law for independent events: P(A and B) = P(A) x P(B) P(A B) = P(A) and P(B A) = P(B) Formula for conditional probability: P(B A) = P(A and B) / P(A) Additionally for Higher tier students: General addition law: P(A or B) = P(A) + P(B) P(A and B)
Formulae sheet/notice Some formulae may be given to students in the assessment. We have taken a different approach to the provision of these formulae according to tier: Foundation tier: no separate formulae sheet. The formula (rates of change) will be given alongside the question Higher tier: separate formulae sheet provided on page 2 of the assessments
Assessment objectives Assessment objectives Weighting AO1 Demonstrate knowledge and understanding, using appropriate terminology and notation, of standard statistical techniques used to: collect and represent data calculate summary statistics and probabilities 55% AO2 Interpret statistical information and results in context and reason statistically to draw conclusions 25% AO3 Assess the appropriateness of statistical methodologies and the conclusions drawn through the application of the statistical enquiry cycle 20%
Breakdown of AOs Paper AO1 AO2 AO3 Total for all AOs 50% 50% 100% Paper 1 Paper 2 Total for GCSE 27.5% 27.5% 55% 3 12.5% 12.5% 25% 3 10% 10% 20% 3
Assessment overview Paper 1 1ST0/1F, 1ST0/1H Paper 2 1ST0/2F, 1ST0/2H Compulsory paper Externally assessed 50% of the total GCSE 1 hour 30 minutes 80 marks Assesses all content Questions on statistical methods and component parts of the SEC Familiar and unfamiliar contexts Short, medium and extended response questions Compulsory paper Externally assessed 50% of the total GCSE 1 hour 30 minutes 80 marks Assesses all content Questions on statistical methods and component parts of the SEC Familiar and unfamiliar contexts Short, medium and extended response questions
Paper overview All content can be assessed on either paper Ramping of questions through each paper, plus ramping within multi-part questions Overlapping tiers with common questions Range of question types: MCQ, short, calculation, open response, extended response Extended response questions: Foundation: there will be at least 3 extended response questions of 5 6 marks each Higher: there will be at least 6 extended response questions of 5 6 marks
Calculators Students must have a scientific calculator with them in both papers which they may use Students are expected to be familiar with the statistical function keys The standard JCQ calculator requirements apply which includes that they may not: Offer symbolic algebraic manipulation Have retrievable information stored in them Use of statistical tables is not required.
Paper 1, Foundation qu. 3 Leyla wants to find out how often people in her town eat in a restaurant. She asked a sample of 30 people how many times they had eaten in a restaurant during the last week. Here are Leyla s results. 3 4 2 1 1 5 1 1 1 2 2 1 2 1 1 2 5 1 3 1 1 4 3 3 1 4 2 1 1 2 (a) Fill in the tally chart for this information and complete the frequency column. (2)
Paper 1, Foundation qu. 3 (b) Write down the mode. (1) (c) Work out the number of people in Leyla s sample who had eaten in a restaurant fewer than 4 times during the last week. (2) (d) Suggest a suitable diagram that Leyla could use to represent her data. (1)
Paper 2, Foundation qu. 2 Tom and Samira want to collect data on the numbers of hours students at their school spend on homework. There are 1100 students at their school. Tom is planning to use a random sample of 50 students. (a) Explain what is meant by a random sample. (1) (b) Describe how Tom could use random numbers to take a random sample of the students at his school. (3) Samira is planning to use a stratified sample that is stratified by school year. (c) Comment on whether Samira s plan is appropriate. (2)
Paper 2, Common qu. 13/4 X and Y are two events. The Venn diagram shows information about the probabilities of events related to X and Y happening. (a) Find (i) the probability of event Y happening (ii) P(X and Y) (iii) P(Y X). (4)
Paper 2, Common qu. 13/4 Two different events A and B are independent. P(A) = 0.8 and P(B) = 0.5 (b) Find P(A and B). (2)
Paper 2, Common qu. 14/5 Gary is going to investigate the amounts of time students spend watching TV. He is going to write a plan for this investigation. His hypothesis is The amount of time that boys spend watching TV is greater than the amount of time that girls spend watching TV . Write down three other things he should include in his plan. Explain why each of these things is appropriate. You must refer to more than one stage of the statistical enquiry cycle. (6)
Paper 1, Higher qu. 11 In a television talent contest, 9 acts were given the following ranks by the judges and by a public telephone vote. (a) Use calculations to determine how much agreement there is between the judges and the public. (5)
Paper 1, Higher qu. 11 Gurdeep was investigating the relationship between the number of points scored and the year practice started for each of 9 acts. This is the scatter diagram he obtained using statistics software.
Paper 1, Higher qu. 11 The statistical software also calculated two correlation coefficients. Spearman s rank correlation coefficient Pearson s product moment correlation coefficient (b) (i) Circle one value in each row below to show the most likely pair of correlation coefficients for this data. Spearman s rank correlation coefficient: 0.9 0.7 0 0.7 0.9 Pearson s product moment correlation coefficient: 0.9 0.7 0 0.7 0.9 (2) (ii) Explain your choice of answers in part (i) (1)
Supporting great Statistics teaching Extensive free support to help you plan, teach, track and assess, and develop the new course This includes free qualification support to download from our website as well as published resources* Plan Teach Develop Track & Assess Free qualification support: http://quals.pearson.com/stats17 * You do not have to purchase any resources to deliver our qualification
Plan To help you plan the new course we are providing: Free support for the qualification: Getting Started Guide Course planner Flexible and adaptable scheme of work Mapping documents Plan Teach Develop Track & Assess
Teach There will be teaching and learning support to help you deliver the new qualification: Plan Free support for the qualification: Teaching points and common misconceptions Support for the statistical enquiry cycle Teach Develop Published resources from Pearson*: Student Book and ActiveBook Track & Assess * You do not have to purchase any resources to deliver our qualification
Track and assess To help you prepare your students for the assessments: Plan Free support for the qualification: Plenty of specimen papers to support formative assessment and mock exams Marked exemplars of student work with examiner commentaries ResultsPlus and examWizard Teach Develop Track & Assess Published resources from Pearson*: Pearson Progression Service * You do not have to purchase any resources to deliver our qualification
ResultsPlus and examWizard ResultsPlus provides the most detailed analysis available of your students exam performance. This free online service helps you identify topics and skills where students could benefit from further learning, helping them gain a deeper understanding of Statistics. examWizard is a free exam preparation tool containing a bank of past Edexcel exam questions, mark schemes and examiners reports, so you can create mock papers, homework or practice tests in minutes.