Overview of Sampling Methods in Markov Chain Monte Carlo

Overview of Sampling Methods in Markov Chain Monte Carlo
Slide Note
Embed
Share

This content covers various sampling methods in Markov Chain Monte Carlo including Rejection Sampling, Importance Sampling, and MCMC Sampling. It delves into representing distributions, drawbacks of Importance Sampling, and the motivation behind Markov Chain Monte Carlo Sampling. The illustrations provided offer insights into adaptive sampling techniques and methods like Metropolis-Hastings and Gibbs sampling.

  • Sampling Methods
  • Markov Chain Monte Carlo
  • Rejection Sampling
  • Importance Sampling
  • MCMC Sampling
novakgr
novakgr Follow

Uploaded on Mar 03, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

Download Presentation

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

E N D

Presentation Transcript

  1. Markov Chain Monte Carlo 10701 Recitation Pengtao Xie 3/3/2025 1

  2. Outline Sampling Methods Rejection Sampling Importance Sampling MCMC Sampling 3/3/2025 2

  3. Outline Sampling Methods Rejection Sampling Importance Sampling MCMC Sampling 3/3/2025 3

  4. How to represent a distribution Closed form representation Gaussian distribution, Dirichlet distribution, Multinomial distribution Sample based representation Draw samples from the distribution and use samples to compute expectation, variance, etc 3/3/2025 4

  5. Outline Sampling Methods Rejection Sampling Importance Sampling MCMC Sampling 3/3/2025 5

  6. May reject a lot of samples 3/3/2025 6

  7. Outline Sampling Methods Rejection Sampling Importance Sampling MCMC Sampling 3/3/2025 7

  8. Importance sampling Drawback: hard to find a Q which matches well with P, may give little importance to most samples 3/3/2025 8

  9. Outline Sampling Methods Rejection Sampling Importance Sampling MCMC Sampling 3/3/2025 9

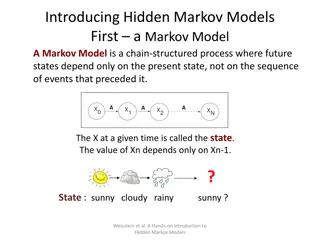
  10. Markov Chain Monte Carlo Sampling Motivation In rejection sampling and importance sampling, Q is fixed. May reject or give little importance to most samples Idea Use an adaptive Q Methods Metropolis-Hastings Gibbs sampling 3/3/2025 10

  11. 3/3/2025 11

  12. 3/3/2025 12

  13. 3/3/2025 13

  14. 3/3/2025 14

  15. 3/3/2025 15

  16. 3/3/2025 16

  17. 3/3/2025 17

  18. 3/3/2025 18

  19. 3/3/2025 19

  20. 3/3/2025 20

  21. 3/3/2025 21

  22. 3/3/2025 22

  23. 3/3/2025 23

  24. Summary Is distribution Q adaptive? NO YES Is accept rate 1? Is accept rate 1? NO YES NO YES Rejection Sampling Importance Sampling Gibbs Sampling MH 3/3/2025 24

  25. References Slides courtesy Professor Eric Xing, 10708 Graphical Models http://www.cs.cmu.edu/~epxing/Class/10708/lectures/lecture16-MC.pdf http://www.cs.cmu.edu/~epxing/Class/10708/lectures/lecture17-MCMC.pdf MCMC theory http://www.cs.cmu.edu/~epxing/Class/10708/lectures/lecture17-MCMC.pdf Slides 15-21 3/3/2025 25

Related


Sampling Methods in Statistical Analysis

Sampling Methods in Statistical Analysis

darci
Dark Matter Search with ATLAS: Active Learning Application

Dark Matter Search with ATLAS: Active Learning Application

alyssia
Non-Probability Sampling Methods

Non-Probability Sampling Methods

novah
Monte Carlo Simulations and Probabilistic Techniques

Monte Carlo Simulations and Probabilistic Techniques

xiomara
Monte Carlo Transport Simulation

Monte Carlo Transport Simulation

katara
Markov Chains and Their Applications in Networks

Markov Chains and Their Applications in Networks

special
Introduction to Markov Models and Hidden Markov Models

Introduction to Markov Models and Hidden Markov Models

claire
Biases in Sampling Methods

Biases in Sampling Methods

selinger_m
Monte Carlo Tree Search (MCTS) Algorithm in Online Planning

Monte Carlo Tree Search (MCTS) Algorithm in Online Planning

maddoxxc
Comprehensive Guidelines for Meth Residue Sampling by Local Health Departments

Comprehensive Guidelines for Meth Residue Sampling by Local Health Departments

guillermi
Non-Probability Sampling Methods

Non-Probability Sampling Methods

ele_poo
MCMC Algorithms and Gibbs Sampling in Markov Chain Monte Carlo Simulations

MCMC Algorithms and Gibbs Sampling in Markov Chain Monte Carlo Simulations

euri_953
Approximate Inference in Bayes Nets: Random vs. Rejection Sampling

Approximate Inference in Bayes Nets: Random vs. Rejection Sampling

pil_g
Monte Carlo Analysis for Uncertainty Assessment

Monte Carlo Analysis for Uncertainty Assessment

jamareon
Variance Reduction Techniques in Monte Carlo Programs

Variance Reduction Techniques in Monte Carlo Programs

jela_859
Beam Polarization Simulation Study for CEPC

Beam Polarization Simulation Study for CEPC

shilling_j
MCMC Sampling Methods in Bayesian Estimation

MCMC Sampling Methods in Bayesian Estimation

rier780
ZMCintegral: Python Package for Monte Carlo Integration on Multi-GPU Devices

ZMCintegral: Python Package for Monte Carlo Integration on Multi-GPU Devices

fike_i
Comparison of Tissue Doses from Various Radionuclides for Radiosynoviorthesis

Comparison of Tissue Doses from Various Radionuclides for Radiosynoviorthesis

dervinma
Monte Carlo Simulation of GEM-Based Neutron Detector and Detector Performance Analysis

Monte Carlo Simulation of GEM-Based Neutron Detector and Detector Performance Analysis

teey962
Stochastic Algorithms: Monte Carlo and Las Vegas Variations

Stochastic Algorithms: Monte Carlo and Las Vegas Variations

lust_zyn
Biomedical Data and Markov Decision Processes

Biomedical Data and Markov Decision Processes

tori_2

More Related Content