Perfect Paths and Precise Landings
Discover the ideal paths for John to walk, ensuring a consistent distance from the hedge and wall, as well as the perfect flight path for a plane to land. Learn about constructing an angle bisector for accurate path-drawing and understanding radii lengths. Explore the concept of equidistance and the construction of circles without changing compass width in this intriguing journey of geometry and precision.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
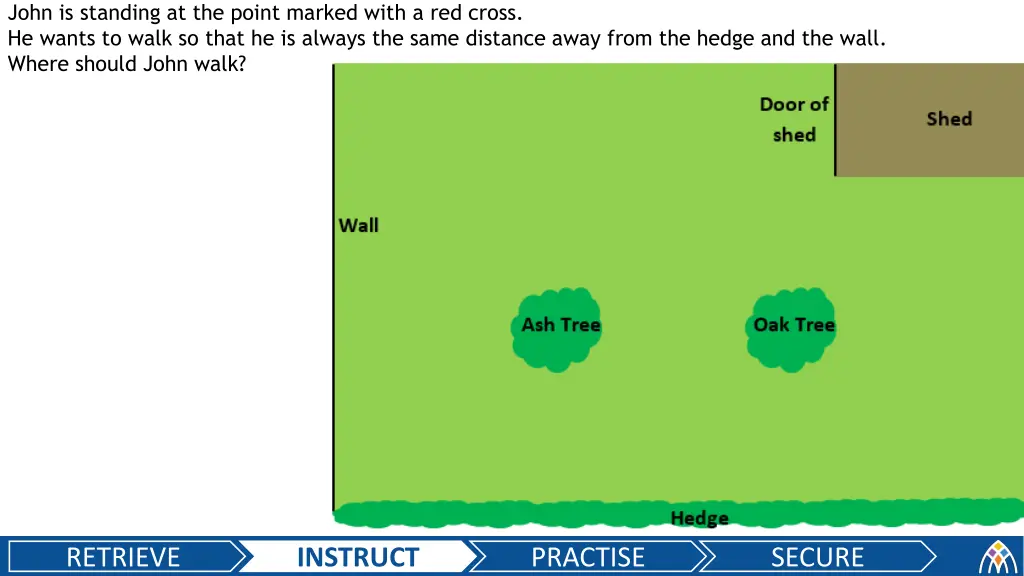
John is standing at the point marked with a red cross. He wants to walk so that he is always the same distance away from the hedge and the wall. Where should John walk? RETRIEVE INSTRUCT PRACTISE SECURE
John is standing at the point marked with a red cross. He wants to walk so that he is always the same distance away from the hedge and the wall. How do you know he is exactly half way between the wall and the hedge? X
John is standing at the point marked with a cross. He wants to walk so that he is always the same distance away from the hedge and the wall. What would be the same if the path had been drawn perfectly? X
EVERY CHILD A READER The ideal flight path for the plane to land is midway between the maximum and minimum angle of descent. What path should the plane take? RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER RETRIEVE DECODE CONNECT VISUALISE SUMMARISE To draw the path accurately we can use a construction known as an angle bisector. INFER What do you think the word bisector means? PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER When constructing an angle bisector RETRIEVE every point on the path drawn is equidistant DECODE from one side as it is from the other. CONNECT VISUALISE SUMMARISE The angle has been perfectly cut in half. INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Which length are radii? RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Without changing the compass width RETRIEVE DECODE Anchor compass on A and draw another circle. CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Without changing the compass width RETRIEVE DECODE Anchor compass on B and draw a third circle. CONNECT VISUALISE SUMMARISE QC is the angle bisector of the acute angle PQR INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER This construction works by creating two congruent triangles RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE 10 RETRIEVE INSTRUCT PRACTISE SECURE
Constructing an angle bisector without drawing full circles Q P R RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Q RETRIEVE DECODE CONNECT VISUALISE SUMMARISE INFER P R PREDICT Both angles will be the same size EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Jiten has attempted to construct an angle bisector of the following angle. RETRIEVE DECODE How can we tell if Jiten is correct or not? CONNECT VISUALISE SUMMARISE What error has Jiten made? INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Independent Practice RETRIEVE Draw these angles in your book and bisect each one. Show your construction lines. DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Challenge Problem RETRIEVE Bisect all 4 angles using the fewest arcs and lines. (Record: 4 arcs, 2 lines) DECODE CONNECT VISUALISE SUMMARISE INFER PREDICT EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
EVERY CHILD A READER Challenge Problem 2 RETRIEVE Draw a triangle and construct the angle bisector of each corner DECODE You should find that the bisectors intersect at a single point inside the triangle! CONNECT Now using the point of intersection as centre, draw the largest possible circle that does not leave the triangle VISUALISE SUMMARISE INFER You should find that the circle touches all three sides of the triangle PREDICT Can you explain why this happens?! This works with anytriangle EXAMINE RETRIEVE INSTRUCT PRACTISE SECURE
