Perimeter and Area in Mathematics
In this chapter, students will gain a clear understanding of the concepts of perimeter and area of closed figures. They will learn to differentiate between perimeter and area and apply relevant formulas to solve various problems. The practical applications of perimeter and area in daily life scenarios are emphasized, highlighting their significance in fields such as farming, construction, sports, and arts.
Uploaded on Feb 19, 2025 | 0 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
SUBJECT -MATHEMATICS CLASS VI CHAPTER - PERIMETER AND AREA Work is Worship
PDF CHAPTER LINK https://drive.google.com/open?id=1pZTOZ5bOF s2lxcmEQz2VQCIzfAVvMGR6 Work is Worship
At the end of the chapter , students will be able to Understand the concept of perimeter and area of a closed figure . Distinguish between the concept of Perimeter and Area in solving different problems as per the requirement. Apply the related formulae in solving different problems . Compare the areas and perimeters of different closed figures. Apply the concept of perimeter and area in solving different problems. Work is Worship
INTRODUCTION We know that plane figures have their closed regions and their boundaries . We need some methods to measure them . The concept of Perimeter and Area arises from this. The idea of Perimeter and Area is widely used in our daily life: A farmer who wants to fence his field or a farmer who wants to plough his field uses this concept. An engineer cannot construct any building without this idea. A sports teacher needs the concept of Perimeter and Area while preparing the tracks. An artist use this idea of perimeter and area to create beautiful designs and different craft work. Work is Worship
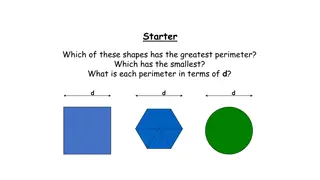
PERIMETER s S If we start from the point s in each figure and move along the line segments, then we again reach the point s , that means we have made a complete shape in each figure. The distance thus covered is known as the perimeter of the figure. The sum of the lengths of all sides of a closed figure or the length of the boundary of a closed figure is called the PERIMETER. Work is Worship
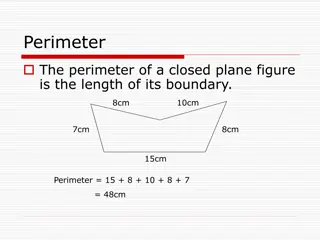
Let us find out the perimeters.. 3cm 3cm Perimeter of the figure = sum of the length of all sides = 3cm+3cm+2.5cm= 8.5cm 2.5cm 6cm 1cm Perimeter of the figure=sum of the length of all sides 2cm = 6cm+6cm+2cm+1cm+1cm=16cm 1cm 6cm 3cm 2cm 4cm Perimeter of the figure = sum of the length of the boundary 3cm 3cm = 2cm +3cm +3cm +3cm = 11cm Work is Worship
PERIMETER OF A RECTANGLE AND A SQUARE l If the length of a rectangle is l and breadth is b, b b then the perimeter = l + b + l + b =2l + 2b =2(l + b) l a If the length of each side of a square is a a a then the perimeter = a + a + a + a=4a a Work is Worship
EXAMPLE - 1 Find the perimeter of the rectangle whose length is 32.5cm and breadth is 27.5 cm. [2] SOLUTION:- Its breadth = 27.5 cm Length of the rectangle = 32.5cm So , its perimeter = 2 x (length + breadth) [0.5] = 2 x (32.5cm + 27.5cm) [0.5] = 2 x 60cm = 120cm [1] The perimeter of the rectangle is 120cm. Work is Worship
EXAMPLE 2 Raghu is having a chessboard whose each side is 26.5cm. Find the perimeter of the chessboard. [2] SOLUTION:- Length of each side of the square = 26.5cm So, its perimeter = 4 x side[0.5] [0.5] = 4 x 26.5cm [1] = 106cm The perimeter of the chess board is 106cm. Work is Worship
EXAMPLE -3 Akshaya goes three times around a rectangular field whose length breadth are 25m and 19m respectively. How much distance does he cover ? [3] Solution : Given , length of the rectangular field= 25m 25 cm Its breadth = 19m So, perimeter of the field = 2 x (l +b) 19 cm = 2 x (25m + 19m) [2] = 2 x 44m = 88m If Akshya goes once around the field, he covers 88m. So ,distance he covers when he moves three times around the field = 3 x 88m= 264m [1] Akshya covers 264 m. Work is Worship
EXAMPLE -4 The length of one side of a square field is 25m. Find the cost of fencing the field at the rate of 118 per metre. [3] Solution : {We know that fencing refers to the perimeter of the field, so here we have to find the perimeter of the field} 25m Given, length of each side of the square field = 25m so, perimeter of the field that is to be fenced = 4 x 25m = 100m [2] Cost of fencing 1m square field = 18 So, cost of fencing 100m square field= 118 x 100m= 1800 [1] The cost of fencing the square field is 1800. Work is Worship
LET US TRY.. Dear students , look at these closed figures .All of them occupy some region of the flat surface. LET US TRY TO FIND OUT WHICH ONE OCCUPIES MORE REGION . (a) (b) (c) Work is Worship
EXPLANATION ON PERIMETER CLICK THE BELOW LINK : https://youtu.be/OUU3n3JAMns Work is Worship
AREA The measure of the surface enclosed by a closed figure is called its AREA. AREA OF A RECTANGLE : l If the length of a rectangle = l b b Its breadth = b Then its area = l x b l AREA OF THE RECTANGLE = LENGTH X BREADTH AREA OF A SQUARE: If the length of each side of a square= a a a Then ,its area = side x side = a x a AREA OF THE SQUARE = SIDE X SIDE N.B. - Unit of area will be in square units. Work is Worship
EXAMPLE - 5 Find the area of a rectangle whose length is 3m and breadth is 75cm. [2] Solution : 3m = 300cm Given, the length of the rectangle = 3m 75 cm = 300cm [0.5] Its breadth = 75cm So ,its area = length x breadth [0.5] = 300cm x 75cm = 22500 sq cm [1] The area of the rectangle is 22500 sq cm. Work is Worship
EXAMPLE -6 Find the area of a square tile whose one side is 15.6 cm. [2] Solution : Given, each side of the square tile = 15.6cm So , its area = side x side [0.5] = 15.6 cm x 15.6 cm 15.6 cm [0.5] = 243.6 sq cm [1] The area of the square tile is 243.6 sq cm Work is Worship
EXAMPLE -7 Vineet wants to polish the floor of a room which is 140cm long and 120cm wide. The charges for polishing the floor is 52 per square metre. What will be the cost of polishing the floor of the room ? [4] Solution : {We know that polishing of the floor refers to the area of the floor. So we have to find the area of the floor} Given , length of the floor = 140 cm = 140 100 =1.4m Its breadth = 120cm = 120 100 = 1.2 m [0.5] So , the area of the floor of the room = length x breadth = 1.4m x 1.2m = 1.68sq m. [1.5] Cost of polishing 1 sq.m. floor = 52 So, cost of polishing 1.68 sq m. floor = 52 x 1.68 = 87.36 [1.5] The cost of polishing the floor is 87.36. [0.5] Work is Worship
EXAMPLE - 8 A square park is to be watered. If one side of the park is 4.2 m, find the area to be watered. [2] Solution : - Given, one side of the square park = 4.2 m So , the area of the park to be watered = side x side [0.5] = 4.2m x 4.2m [0.5] = 17.64 sq.m. [1] 17.64 sq.m. area of the park is to be watered. Work is Worship
SOME MORE FORMULAE RECTANGLE: - Length = ???? ?????? ???? ????? Breadth = Length = ????????? - breadth 2 Breadth =????????? - length 2 SQUARE:- Side =????????? 4 Side = Area Work is Worship
EXAMPLE - 9 A rectangular garden is 230m long and its area is 13,800sq. m. Find the width of the garden. [2] SOLUTION:- Given, the area of the rectangular garden= 13,800sq. m. Its length= 230 m ???? ????? [0.5] = 13800 ??? 230? [1.5] = 60m The width of the garden is 60m. So, its width = Work is Worship
EXAMPLE - 10 The length of a rectangle is 2.5m and its perimeter is 800cm.Find its breadth. [3] Solution:- Given , the perimeter of the rectangle = 800cm Its length = 2.5m = 2.5m x 100= 250cm [0.5] So, its breadth = ????????? 2 - length [0.5] = 800?? 2 - 250cm = 400cm 250cm= 150cm [2] The breadth of the rectangle is 150cm. Work is Worship
EXAMPLE-11 The area of a square of side 8cm is the same as that of a rectangle of length 32cm. What is the breadth of the rectangle? [4] Solution : - Given , each side of the square = 8cm So, the area of the square = side x side = 8cm x8cm =64 sq.cm. [1.5] According to the question, the area of the rectangle = the area of the square [1] = 64 sq.cm. Length of the rectangle = 32cm ???? ????? So, its breadth = = 64??.??. 32?? = 2cm [1.5] The breadth of the rectangle is 2cm. Work is Worship
EXAMPLE -12 What will happen to the area of the square when [4] (i) its side is doubled? Solution : - Let each side of the square = 1 unit so , its area = side x side = 1unit x 1 unit = 1 sq. unit. [1] When its side is doubled, its new side = 2 x 1unit = 2 units So, its new area = side x side = 2 units x 2 units = 4 units = 4 x old area [1] The area of the square becomes 4 times the old area when the side is doubled. Work is Worship
EXAMPLE 12 CONTD. (ii)its side is halved ? Solution :- 2unit when its side is halved, its new side = 1 So, its new area = side x side = 1 2 unit x 1 2 unit [1.5] = 1 4 sq.unit. = 1 4 of the old area When the side is halved, area becomes one fourth. [0.5] Work is Worship
EXAMPLE - 13 A street lane is to be paved with tiles of length 12cm and breadth 10cm.If the length of the lane is 240m and its breadth is 12m, find the no of tiles needed. [4] Solution : - Length of each tile = 12cm Its breadth = 10cm So, area of each tile = length x breadth = 12cm x 10cm = 120 sq.cm. [1.5] Length of the lane = 240m = 24000 cm Its breadth = 12m = 1200cm So, the area of the lane = length x breadth = 24000cm x 1200cm = 28800000 sq .cm. [1.5] So, number of tiles needed = ???? ?? ? ? ???? ???? ?? ??? ???? = 28800000 ??.?? 120 ??.?? 240000 tiles needed to pave the lane. = 240000 [1] Work is Worship
EXPLANATION ON AREA CLICK THE BELOW LINK : https://youtu.be/ozO6_1NoGu8 Work is Worship
ACTIVITY - 1 In this activity students are required to collect five leaves of different shapes and estimate their area by drawing their outlines on graph sheet. They have to arrange their areas in descending order in a table. Materials required :- leaves, graph sheet, sketch pens Important points: - Area of one full square will be counted as 1sq.unit. Ignore portions of the area that are less than half a square. If more than half of a square is there, it will be counted as one square. If exactly half of the square, it will be taken as 1 2 sq. unit. Work is Worship
TRY TO EVALUATE YOURSELF. The length of the boundary of a closed figure is called ----------- . The amount of surface enclosed by a figure is called ------------ . Perimeter of a triangle with sides 4.5cm, 6.02cm ,5.38cm is --------------- . Area of a square of side 7 cm is ---------------- . If the perimeter of a rectangle is 30 cm and its breadth is 6cm, then its length is ------------- . To find the cost of painting a wall , we need to find the ----------- of the wall. To find the cost of framing a photo, we need to find the --------- of the photo. If the area of a square is 100 sq.cm. , then its side is ----------- . To find the cost of fencing a field , we need to find the ----------- of the field. Work is Worship
TIME TO RECAPITULATE The length of the boundary of a closed figure is called the perimeter of the figure. The amount of surface enclosed by a closed figure is called the area. Perimeter of a square = 4 x side Perimeter of a rectangle = 2 x ( length + breadth) Area of a square = side x side Area of a rectangle = length x breadth Side of a square = ????????? 4 Side of a square = ???? Length of a rectangle = ????????? 2 breadth of a rectangle = ????????? 2 Length of a rectangle = ?????? ???? ????? - breadth - length ???? Breadth of a rectangle = Work is Worship
INTEGRATING ART WITH PERIMETER AND AREA Work is Worship
ACTIVITY - 2 In this activity, students have to design a zoo in a graph sheet by using the concept of perimeter and area as the example shown. They need to calculate the perimeter and area of each segment of the zoo and arrange them in a tabular form. Materials required : - Graph sheet, crayons and other drawing materials. Work is Worship
LEARNING OUTCOMES :- Students will be able to calculate the perimeter and area of different plane figures. Students will be able to apply this concept in different project works. They will also be able to use this concept in different art and craft works. Work is Worship
CONCEPT MAPPING PERIMETER AND AREA PERIMETER AREA The length of the boundary of a closed figure is called Perimeter. The amount of surface enclosed by a closed figure is called Area. Perimeter of a rectangle = Perimeter of a square = Area of rectangle = l x b Area of a square = Side x Side 4 x Side 2x (length x breadth) Breadth Length Side = Area Side = ????????? Length =????????? Breadth = ????????? 2 ???? ????? ???? ?????? = = - l - - b 4 2 Work is Worship