Phragmns Sequential Rule 1894 - Election Process Explained
Phragmns Sequential Rule, introduced in 1894, outlines the process of electing committee candidates by filling voters' virtual bank accounts until a candidate garners $1 in total support. This continues until a set number of candidates have been elected. The rule dictates the cost and method of electing candidates in a systematic manner.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
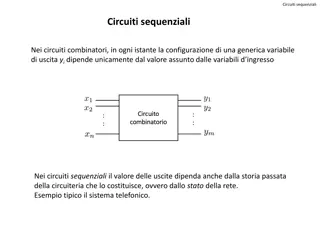
Phragmns Sequential Rule (1894) It costs $1 to elect a candidate to the committee. Each voter has a virtual bank account, initially empty. We slowly fill up the bank accounts until some candidate has supporters who have $1 in total. We elect such a candidate and take the supporters money away. Finish when k candidates have been elected.
? = 12 4 4 5 5 6 6 10 10 14 14 18 18 3 3 9 9 13 13 17 17 2 2 8 8 12 12 16 16 1 1 7 7 11 11 15 15 ?1 ?1 ?2 ?2 ?3 ?3 ?4 ?4 ?5 ?5 ?6 ?6
? = 12 4 4 5 5 6 6 10 10 14 14 18 18 3 3 9 9 13 13 17 17 2 2 8 8 12 12 16 16 1 1 7 7 11 11 15 15 ?1 ?1 ?2 ?2 ?3 ?3 ?4 ?4 ?5 ?5 ?6 ?6
? = 12 4 4 5 5 6 6 10 10 14 14 18 18 3 3 9 9 13 13 17 17 2 2 8 8 12 12 16 16 1 1 7 7 11 11 15 15 ?1 ?1 ?2 ?2 ?3 ?3 ?4 ?4 ?5 ?5 ?6 ?6
? = 12 4 4 5 5 6 6 10 10 14 14 18 18 3 3 9 9 13 13 17 17 2 2 8 8 12 12 16 16 1 1 7 7 11 11 15 15 ?1 ?1 ?2 ?2 ?3 ?3 ?4 ?4 ?5 ?5 ?6 ?6
? = 12 4 4 5 5 6 6 10 10 14 14 18 18 3 3 9 9 13 13 17 17 2 2 8 8 12 12 16 16 1 1 7 7 11 11 15 15 ?1 ?1 ?2 ?2 ?3 ?3 ?4 ?4 ?5 ?5 ?6 ?6
? = 12 4 4 5 5 6 6 10 10 14 14 18 18 3 3 9 9 13 13 17 17 2 2 8 8 12 12 16 16 1 1 7 7 11 11 15 15 ?1 ?1 ?2 ?2 ?3 ?3 ?4 ?4 ?5 ?5 ?6 ?6
? = 12 4 4 5 5 6 6 10 10 14 14 18 18 3 3 9 9 13 13 17 17 2 2 8 8 12 12 16 16 1 1 7 7 11 11 15 15 ?1 ?1 ?2 ?2 ?3 ?3 ?4 ?4 ?5 ?5 ?6 ?6
? = 12 4 4 5 5 6 6 10 10 14 14 18 18 3 3 9 9 13 13 17 17 2 2 8 8 12 12 16 16 1 1 7 7 11 11 15 15 ?1 ?1 ?2 ?2 ?3 ?3 ?4 ?4 ?5 ?5 ?6 ?6
? = 12 4 4 5 5 6 6 10 10 14 14 18 18 3 3 9 9 13 13 17 17 2 2 8 8 12 12 16 16 1 1 7 7 11 11 15 15 ?1 ?1 ?2 ?2 ?3 ?3 ?4 ?4 ?5 ?5 ?6 ?6
? = 12 4 4 5 5 6 6 10 10 14 14 18 18 3 3 9 9 13 13 17 17 2 2 8 8 12 12 16 16 1 1 7 7 11 11 15 15 ?1 ?1 ?2 ?2 ?3 ?3 ?4 ?4 ?5 ?5 ?6 ?6
? = 12 4 4 5 5 6 6 10 10 14 14 18 18 3 3 9 9 13 13 17 17 2 2 8 8 12 12 16 16 1 1 7 7 11 11 15 15 ?1 ?1 ?2 ?2 ?3 ?3 ?4 ?4 ?5 ?5 ?6 ?6
? = 12 4 4 5 5 6 6 10 10 14 14 18 18 3 3 9 9 13 13 17 17 2 2 8 8 12 12 16 16 1 1 7 7 11 11 15 15 ?1 ?1 ?2 ?2 ?3 ?3 ?4 ?4 ?5 ?5 ?6 ?6