Practical Applications of Combinations in Committee Selections
Explore the practical applications of combinations in forming committees based on specific criteria such as the number of men and women to be included. Learn how to calculate different committee configurations from given groups of individuals and subjects.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
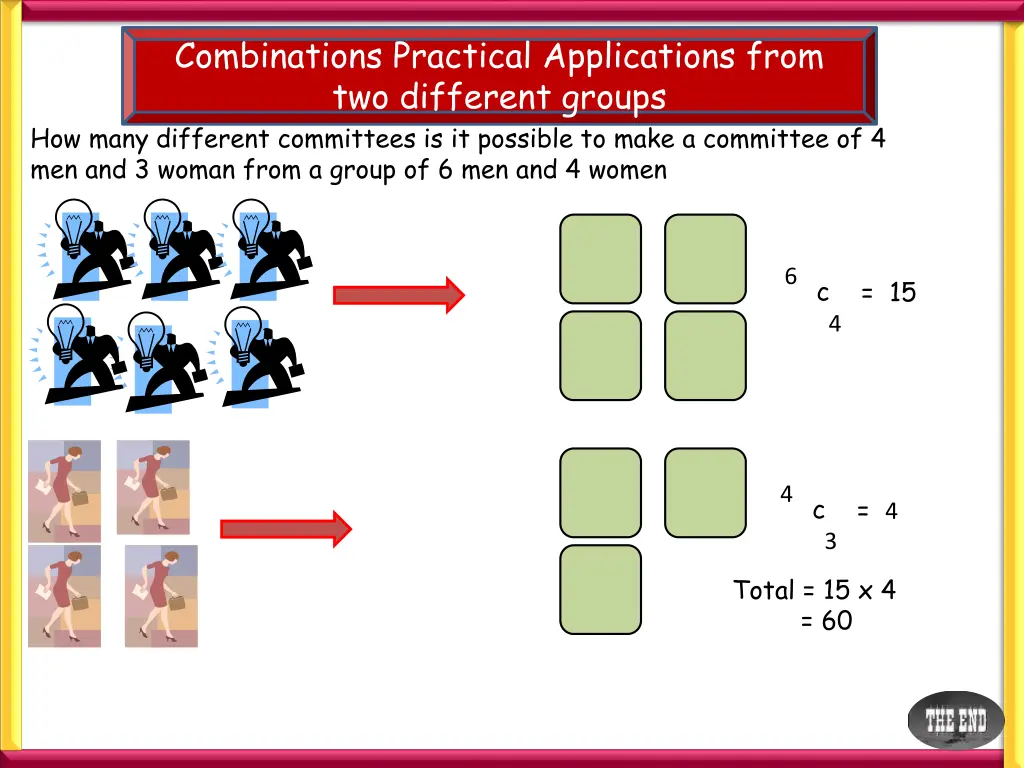
Combinations Practical Applications from two different groups How many different committees is it possible to make a committee of 4 men and 3 woman from a group of 6 men and 4 women 6 c = 15 4 4 c = 4 3 Total = 15 x 4 = 60 Total = 15 x 4 = 60
In a certain school the examination subjects for senior students are grouped as follows: As well as taking all three of the compulsory subjects, each student must choose one subject from Block A, two from Block B and one from Block C. (i) In choosing two subjects from Block B, how many different selections are possible? (ii) In choosing the full range of subjects, how many different selections are possible? (iii) One student has already decided to do German and construction studies. How many different selections of the remaining subjects are possible for this student?
In a certain school the examination subjects for senior students are grouped as follows: As well as taking all three of the compulsory subjects, each student must choose one subject from Block A, two from Block B and one from Block C. (i) In choosing two subjects from Block B, how many different selections are possible? 4c2= 6 (ii) In choosing the full range of subjects, how many different selections are possible? 4c2= 6 = 2 x 6 x 3 = 36 2 c1= 2 3c1 = 3 Total (iii) One student has already decided to do German and construction studies. How many different selections of the remaining subjects are possible for this student? 3c1 = 3 x 3 = 9 3 c1= 3 = 3 Total
12.6 Practical Applications from two different groups How many different ways is it possible to make a committee of 5 people from a group of 4 men and 6 women if (i) There are no restrictions (ii) It must include one woman and one man (iii)It must include 4 men (iv) It must include at least 3 women (i) 10c = 252 5
(ii) It must include one woman and one man 8 c = 56 3
(ii) It must include 4 men 6 c = 6 1
(iv) It must include at least 3 women 3 women 7 c = 21 2 4 women 6 c = 6 1 Total = 21 + 6 = 27 5 women 5 c = 0 0
