Projectile Motion Analysis for Determining Displacement, Velocity, and Time
Explore the principles of projectile motion to calculate horizontal and vertical displacement, velocity, peak time, and total flight time. Understand how gravity influences projectile trajectories and the impact of launch angles on range.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Launcher 101 ANALYZING PROJECTILE MOTION TO DETERMINE HORIZONTAL AND VERTICAL DISPLACEMENT, VELOCITY, TIME TO REACH THE PEAK OF THE TRAJECTORY, AND TOTAL TIME OF FLIGHT
Components of Launcher Components of Launcher A projectile is any object that moves through the air or space, acted on only by gravity (and air resistance, if any). A ping pong ball shot from a launcher, a stone thrown into the air, are two examples of projectiles. Paths are surprisingly simple and can be resolved into horizontal and vertical components.
Projectile Motion Projectile Motion The horizontal component of motion for a projectile is just like the horizontal motion of a ball rolling freely along a level surface without friction. The vertical component of a projectile s velocity is like the motion for a freely falling object. The horizontal component of motion for a projectile is completely independent of the vertical component of motion.
Gravities Influence Gravities Influence Projectile motion is dependent upon its initial velocity. The greater the initial velocity, the farther away it will land. Example: How much effort you put into moving your hand and prior to releasing the stone will determine how far the stone will move away form you.
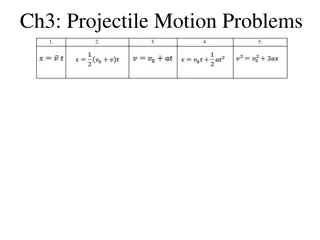
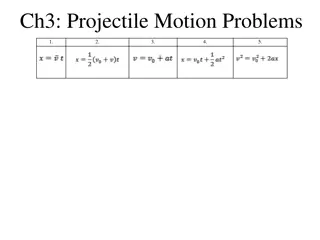
Projectiles Launched at an Angle If there were no gravity the cannonball would follow the straight-line path shown by the dashed line. path shown by the dashed line. If there were no gravity the cannonball would follow the straight-line But because of gravity it falls beneath this line the same vertical distance it would fall if it were released from rest. distance it would fall if it were released from rest. But because of gravity it falls beneath this line the same vertical The vertical displacement (y) can be determined using the following equation, where ?? is the initial vertical component of velocity. ? = ??+ ? + 0.5 ? ?2
Projectile Height Projectile Height The velocity of a projectile is shown at various points along its path. Remember that the vertical component changes while the horizontal component does not. Air resistance is neglected.
Projectile Range Projectile Range The angle at which the projectile is launched affects the distance that it travels. Provided both projectiles have the same launching speed. Lower launch angle results in greater horizontal component Higher launch angle results in greater vertical component 45o angle results in equal horizontal and vertical components The horizontal component is less, so the range is less.
Neglecting Air Resistance Neglecting Air Resistance The same range is obtained for two different projection angles angles that add up to 90 . Maximum range is usually attained at an angle of 45 .
Projectile Speed Projectile Speed Without air resistance, a projectile will reach maximum height in the same time it takes to fall from that height to the ground. The deceleration due to gravity going up is the same as the acceleration due to gravity coming down. The projectile hits the ground with the same speed it had when it was projected upward from the ground.
Air Resistance Air Resistance In the presence of air resistance, the path of a high-speed projectile falls below the idealized parabola and follows the solid curve.