Quantum Rules in Physical Chemistry Equilibrium
Explore the principles of physical chemistry, including matter, logic, change, equilibrium, and structure. Delve into the origins of quantum rules, studying the mass of protons and electrons, and the behavior of pendulums in relation to quantum energy. Discover the fascinating world of molecular energy levels, vibration, and photon wavelengths. Gain insights into quantization of energy in different types of motion and the Boltzmann distribution in thermal agitation. Enhance your knowledge of quantum effects in vibrating molecules through this comprehensive study.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
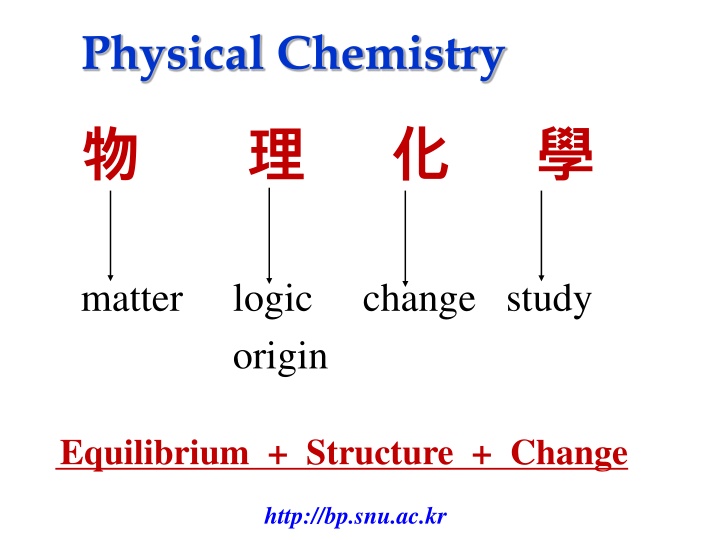
Physical Chemistry matter logic change study origin Equilibrium + Structure + Change http://bp.snu.ac.kr
Introduction Mass of proton = 2000 mass of electron Electrons contribute very little to the total mass of the atom, but occupy an appreciable volume, and are responsible for the atomic bulk. The Quantum Rules: The energy of an object cannot be changed by an arbitrary amount. pendulum or spring Consider a pendulum. 1 1 g k = = 0 , h h h h : Planck s constant natural frequency 2 2 l m http://bp.snu.ac.kr 2
Figs. 8.17 and 8.18 Fig. 15.3 Harmonic Oscillator The array of molecular energy levels used to calculate the molecular partition function. Phonon = Lattice Vibration http://bp.snu.ac.kr 3
Pendulums of different natural frequencies accept and give up quanta of different sizes, and the higher the natural frequency the larger the quantum energy. h = 4.1357 10 eV s if = 1 Hz , h = 4.1357 10 eV too small to be detected. Only when very high frequency motions are involved, the quantum energy h becomes large enough to give rise to significant effects. A mass on a spring oscillating with simple harmonic motion: Phonon = 1013Hz 1 k = 2 m When the mass is that of an atom, the frequency is extremely high, and so we must be prepared for significant quantum effects in vibrating molecules. http://bp.snu.ac.kr 4
Photon Wavelength, (a) (b) Figure F.8 The wave is shown travelling to the right at a speed c. Wavelength and frequency are related by = c. http://bp.snu.ac.kr 5
Figure F.4 Quantization of the energy of different types of motion. Free translational motion in an infinite region is not quantized, and the permitted energy levels form a continuum. Rotation is quantized, and the separation increases as the state of excitation increases (moment of inertia of the molecule). Vibrational motion is quantized, but note the change in scale between the ladders. Electronic energy levels are quantized, and the separations are typically very large (of the order of 1 eV). http://bp.snu.ac.kr 6
Chapter 15 F.5(a) Boltzmann Distribution ConsiderThermalAgitation. Some molecules occupy the lowest energy levels, others will be in the excited levels. Not all reach the higher levels: there is a predominance of molecules in the lower, less energetic states, but the tail of the distribution gets larger and penetrates further into the high energy region as the temperature is raised. (Figure F.5) N ( ) i = exp / E E RT (F.9) ________________ i j N j , E E : molar energies at states i and j R: gas constant, 8.314 JK 1 T: absolute temperature i j Boltzmann s Constant: kB= 8.617 10 eV/K http://bp.snu.ac.kr 7
Low T High T Figure F.5 The Boltzmann distribution predicts that the population of a state decreases exponentially with the energy of the state. Energy (a) At low temperatures, only the lowest states are significantly populated. (b) At high temperatures, there is significant population in high- energy states as well as in low- energy states. At infinite temperature (not shown), all states are equally populated. Population -2014-3-4 http://bp.snu.ac.kr 8
Nuclear excitation Core-electron excitation Electronic excitation Molecular vibration Molecular rotation Wavelength/m Figure F.9 The regions of the electromagnetic spectrum and the types of excitation that give rise to each region. Visible Light: ~400 700 nm ~2 3 eV ~1015Hz http://bp.snu.ac.kr 9
Chapter 15 Figure F.7 The essential content of the Maxwell distribution of molecular speeds. Note how the maximum in the distribution moves to higher speeds as the temperature is increased or, at constant temperature, we consider species of decreasing mass. The distribution also becomes wider as its peak moves to higher speeds. http://bp.snu.ac.kr 10
The average kinetic energy of 1 mol of particles from the Maxwell- Boltzmann distribution = RT. Equipartition theorem of classical physics: 3 _____ F.5(b) Chapters 15 & 16 2 __ 1 average energy of different modes of motion = RT. 2 1 three dimensional translational modes = 3 RT 2 Association of atoms and molecules 1. Ionic bond 2. Covalent bond 3. Metallic bond: an assembly of cations (Cu2+) immersed in a sea of electrons 4. van der Waals force: (a) due to polar attraction (b) due to instantaneous electric dipoles (c) due to hydrogen bonding http://bp.snu.ac.kr 11
F.3 The State of Matter Solid State: Crystal or Amorphous (Glass) 1. Morphology: crystal s external appearance 2. Crystal defects: the breaks in the uniformity of array 3. Liquid crystals: van der Waals attraction is so weak that the crystals possess virtually no rigidity. Liquid State The ordered structure of solid Less-Ordered fluid function atomic correlations Diffuse atomic correlations Melting Point http://bp.snu.ac.kr 12
The Ability to Flow The number of molecules with enough energy to move follows a Boltzmann distribution. ( RT Ea/ exp Activation Energy Activation Enthalpy ) Fluidity where E is the energy to be overcome. Viscosity where E is of the same order as the intermolecular binding energy. ( ) + exp E/ RT Gas Phase The average distance between molecules is normally large relative to their diameter. At low pressure, the intermolecular interactions are likely to be negligible, and the gas satisfies the ideal gas law: p: pressure n: amount of gas T: absolute temperature V: volume = = pV nRT http://bp.snu.ac.kr 13
3 The mean kinetic energy of 1 mol of gas = RT The kinetic energy of 1 mol of gas = 2 1 2 m v N A 2 N : Avogadro s number A 2v 2v : average value of 3 1 3 1 _______ 2 2 RT = 2 m v N = 2 k T m v A 2 2 RT B 3 mN = 2 v A 3 kT 3 RT = = 2 v : Root mean square speed mN m A R k = N A http://bp.snu.ac.kr 14
Transformations of Matter Can it occur? Thermodynamics How fast does it occur? Kinetics The probability that when the collision occurs it does so with sufficient energy to react will be determined by the Boltzmann distribution. Ea: necessary energy (activation energy of the reaction) Rate of reaction (rate of collision) (probability that collision carries enough energy) (___ RT E Arrhenius equation ) exp Z T a http://bp.snu.ac.kr 15
International System of Units (SI) CGS (cgs) or MKS cm g s A K mol cd J/s 1 eV = 1.602 10-19J = 1.602 10-12erg http://bp.snu.ac.kr 16
_________________________________________ ______________________ http://bp.snu.ac.kr 17
___/_atom _______ 105J/mol _____________ http://bp.snu.ac.kr 18
Problems from Chap. Fundamentals F1.1(a) F1.3(a) F2.1(a) F3.1(a) F3.2(a) F3.3(a) F3.4(a) F4.1(a) F4.2(a) F5.2(a) F5.4(a) F5.6(a) F6.1(a) F6.2(a) F6.3(a) -2014-3-6 http://bp.snu.ac.kr 19
