Rational and Irrational Numbers in the Real Number System
Explore the classification of numbers within the Real Number System, distinguishing between rational and irrational numbers. Learn how to identify them and their place in the number hierarchy, including subsets like Integers, Whole Numbers, and more.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
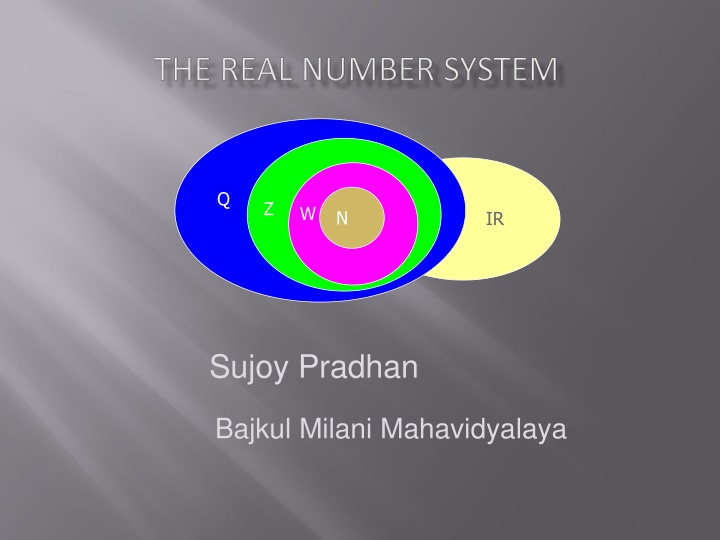
Q Z W N IR Sujoy Pradhan Bajkul Milani Mahavidyalaya
8.NS: Know that there are numbers that are not rational and approximate them by rational numbers. 8.NS.1: Understand informally that every number has a decimal expansion; the rational numbers are those with decimal expansions that terminate in zeros or eventually repeat. Know that other numbers are called irrational numbers.
How can you identify whether numbers are rational or irrational, and where do they classify within the number system? Q Z W IR N
The Real Number System is made up of a set of rational and irrational numbers. It has at five subsets: a. Rational Numbers (Q) b. Integers (Z) c. Whole Numbers (W) d. Natural Numbers (N) e. Irrational Numbers (IR)
Real Numbers consists of all rational and irrational numbers. It includes any number that can be written as a fraction, mixed numbers, terminating and repeating decimals, whole numbers, integers, square and cube roots. O
Rational Numbers consists of integers, terminating, and repeating decimals. It can also be expressed as a fraction, perfect squares and perfect cubes. { -3, -2, -1, 0, 1, 2, 3, }
Integers consist of natural numbers, their opposites (negative # s), and zero. It does not include fractions or decimals. All whole numbers are integers. For example: { -3, -2, -1, 0, 1, 2, 3, )}
Whole numbers consist of natural numbers and zero. {0, 1, 2, 3, 4, } Natural numbers are all the counting numbers. {1, 2, 3, 4 }
Terminating Decimals are rational numbers that stops before or after the decimal point. For example: 5.0, 2.75, .40, .0001 etc. Repeating Decimals are rational numbers that repeats after the decimal point. For example: .3333 , ,
Irrational numbers consist of numbers that are non- terminating and non-repeating decimals. They cannot be express as a fraction! Pi is a great example of an irrational number http://www.joyofpi.com/pi.html .001, .0011, .00111, .001111 etc
Real Numbers Rational Numbers (Fractions & Perfect Squares/Cubes) Irrational Numbers Terminatin g Decimals Repeating Decimals Integers Non-Terminating And Non-Repeating Decimals Whole Numbers Negative # s Natural # s Zero
What did you learn in this lesson? What are some important facts to remember about the real number system? Is there something within the lesson that you need help on?
1.) How are the natural and whole numbers different? 2.) How are the integers and rational numbers different? 3.) How are the integers and rational numbers the same? 4.) How are integers and whole numbers the same? 5.) Can a number be both rational and irrational? Use the diagram to explain your answer.
Answer True or False to the statements below. If the statement is False, explain why. 6.) 5 is a rational number. _______ 7.) is rational. _______ 8.) is a natural number __________ 9.) is an integer. _______ 10.) 2.434434443 is a rational number.____________




