Rectangle Properties and Transformations Explained
Explore the concept of rectangles through identifying missing coordinates, calculating perimeter, and investigating translations. Challenge yourself to draw rectangles with the same dimensions in different locations and understand the changes in coordinates through translations. Engage in discussions about the effects of translations on vertices and how they impact the x and y-coordinates.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
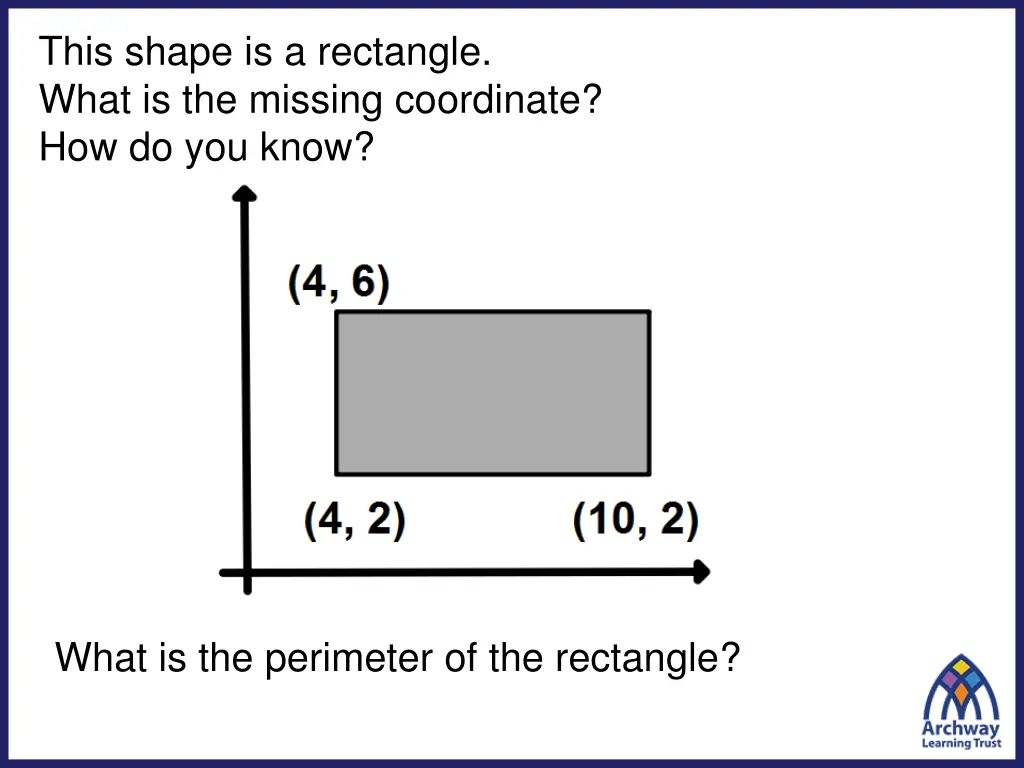
This shape is a rectangle. What is the missing coordinate? How do you know? What is the perimeter of the rectangle?
Draw another rectangle with the same dimensions somewhere else on your grid. What are its coordinates? Draw one in each quadrant and write down the coordinates of the vertices. Compare yours with your neighbour s.
Challenge: Can you write down the coordinates of a another rectangle with the same dimensions that isn t on your grid? How do you know it s correct?
Challenge 2: If another rectangle with the same dimensions has coordinate A (a , b) what are the other coordinates? What if the rectangle had coordinate D (c, d)?
If I translate this rectangle two squares down, what will the coordinates of the vertices be now? How have they changed?
If I translate the rectangle one square to the right, what will the coordinates of the vertices be now? How have they changed?
If I translate the rectangle five squares to the left, what will the coordinates of the vertices be now? How have they changed?
If I translate the rectangle 4 squares to the left, and 3 square up what will the coordinates of the vertices be now?
If I translate the rectangle a squares to the left, and b square up what will the coordinates of the vertices be now?
Discuss with your partner what you think the missing words are and why. In general: When a shape is translated right the x-coordinates increase. When a shape is translated left the x-coordinates decrease. When a shape is translated up the y-coordinates increase. When a shape is translated down the y-coordinates decrease.
This instruction can also be communicated using a vector. The vector for this translation would look like this: ? ?
? ? What do you think the vector for this translation will be?
? ? The x-coordinates decrease by 5
? ? What do you think the vector for this translation will be?
? ? The y-coordinates decrease by 2
? ? What do you think the vector for this translation will be?
? ? The x-coordinates decrease by 4 The y-coordinates increase by 3
Title: Translation Vectors A translation can be described using a column vector. A column vector describes how far and in which direction to move an image. The top value tells us how far and it which direction the x coordinates move ? ? The bottom value tells us how far and it which direction the y coordinates move
In your books: Describe, in words, the translations these vectors represent. 0 2 2 0 2 2 2 2
Mark your work: 0 2 Two units up 2 0 Two units to the left 2 2 Two units right and two units down 2 2 Two units left and two units up
Vector nakes and L A D D E R S
Rules for the game. Roll the dice and move your counter the number of squares shown on the dice. If you land on a blank numbered square, that ends your go. If you land on a vector, follow it. Then it is the end of your go. The winner is the first person to get to the finish in the exact number of moves.
( ) -4 ( ) -1 ( ) 0 100 99 98 97 96 95 94 93 92 91 2 2 -2 FINISH ( ) -1 ( ) -1 ( ) -6 81 82 83 84 85 86 87 88 89 90 1 3 -2 ( ) 1 ( ) -2 ( ) -1 80 79 78 77 76 75 74 73 72 71 3 0 1 ( ) -1 ( ) 2 ( ) -2 61 62 63 64 65 66 67 68 69 70 2 -1 ( ) 2 ( ) -1 60 59 58 57 56 55 54 53 52 51 2 -6 ( ) 3 ( ) -1 ( ) -2 41 42 43 44 45 46 47 48 49 50 1 3 -1 ( ) -1 ( ) 1 ( ) -1 ( ) 2 40 39 38 37 36 35 34 33 32 31 -1 -2 -4 0 ( ) -2 ( ) 5 21 22 23 24 25 26 27 28 29 30 -1 1 ( ) 3 ( ) 2 ( ) -1 20 19 18 17 16 15 14 13 12 11 0 1 5 ( ) 2 ( ) 2 ( ) 1 1 2 3 4 5 6 7 8 9 10 -1 2 -4 START
