Rectangles and Integer Sides: AMC Problem Solving
Analyze a geometric problem involving a rectangle with integer sides and a diagonal stripe. By determining the relationship between the shaded and white areas, conclude the perimeter of the rectangle. Through step-by-step deductions, the solution reveals the rectangle's dimensions and perimeter.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
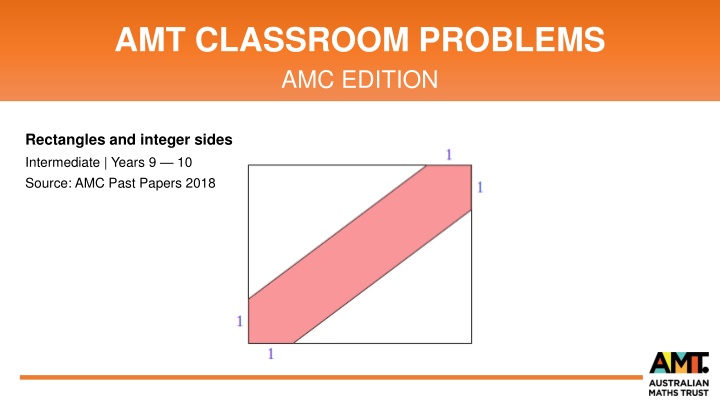
AMT CLASSROOM PROBLEMS AMC EDITION Rectangles and integer sides Intermediate | Years 9 10 Source: AMC Past Papers 2018
Rectangle and integer sides AMC PROBLEM A rectangle with integer sides has a diagonal stripe which starts 1 unit from the diagonal corners, as in the diagram. The area of the stripe is exactly half of the area of the rectangle. What is the perimeter of this rectangle? a) 14 b) 16 c) 18 d) 20 e) 22
Rectangle and integer sides AMC PROBLEM Alternative 1 Hence a) 14
Rectangle and integer sides AMC PROBLEM Alternative 2 Slide the triangles together and shade the rest of the rectangle, as 1 shown. Since the original rectangle was half shaded, so is this diagram. One solution that can be observed is a 2 x 3 white rectangle inside a 3 x 4 rectangle. We claim that this is the only possibility. The white rectangle must be more than 1 high, since otherwise it fits inside the shaded area. So the original rectangle is more than 2 high. Similarly, the original rectangle is more than 2 wide. Slice the shaded and white areas into the rectangles shown on the left. Since A = X, it follows that B = Y . Hence a) 14
Rectangle and integer sides AMC PROBLEM Alternative 2 | Continued Slice the shaded and white areas into the rectangles shown on the left. Since A = X, it follows that B = Y . Now slice areas B and Y into the rectangles shown on the right. Then C= Z, so that D = 2. Since D has integer sides, it can only be 2 x 1. Consequently the original rectangle is 4 x 3, with perimeter 2 x 4 + 2 x 3 = 14, Hence a) 14