Rotational Kinetic Energy
Learn about the principles of rotational kinetic energy, including translational and rotational components. Solve problems involving kinetic energy, work, and angular velocity. Explore concepts through examples and whiteboards. Understand how to calculate the total kinetic energy and work done in rotational systems.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
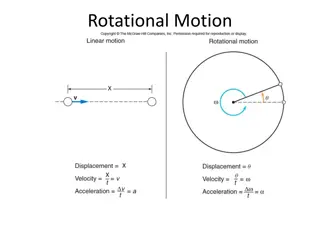
Rotational KE Two types of kinetic energy: Translational: Ekin= 1/2mv2 Rotational: Ek rot = 1/2I 2 Of course a rolling object has both Work: W = Fs W =
Example: A 23.7 kg 45 cm radius cylinder is rolling at 13.5 m/s at the bottom of a hill. What is its translational kinetic energy? What is its rotational kinetic energy? What is the total kinetic energy? What was the height of the hill?
Whiteboards: Rotational KE 1-6
What is the rotational kinetic energy of an object with an angular velocity of 12.0 rad/s, and a moment of inertia of 56.0 kgm2? 4.0 x 103 J
What must be the angular velocity of a flywheel that is a 22.4 kg, 54 cm radius cylinder to store 10,000. J of energy? 78 rad/s
What is the total kinetic energy of a 2.5 cm diameter 405 g sphere rolling at 3.5 m/s? 3.5 J
What work do you do if you exert 14.0 mN of torque through 3.10 rotations? solution 273 J
If you exert 14.0 mN of torque through 3.10 rotations on a potter s wheel that is a 26.0 kg, 68.0cm diameter uniform cylinder, what will be the final angular velocity? solution 19.1 rad/s
A tangential friction force of 2.30 N slows down a 26.0 kg 68.0 cm diameter potter s wheel. (That is a uniform cylinder) If it was originally going at 71.0 RPM, in how many rotations will it stop? solution 8.45 rot