Rounding-based Moves for Metric Labeling
Within the realm of metric labeling, this study delves into rounding-based moves for effective labeling strategies. The exploration covers various potentials, including unary and pairwise, emphasizing the distinguishing energy factor. Move-making algorithms are discussed, highlighting linear programming relaxation for accuracy. Additionally, the expansion algorithm and binary indicators are examined for efficient label assignment.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Rounding-based Moves for Metric Labeling M. Pawan Kumar Center for Visual Computing Ecole Centrale Paris
Metric Labeling Post Random variables V = {v1, v2, , vn} Label set L = {l1, l2, , lh} Labeling y Ln Labelings quantatively distinguished by energy E(y) Unary potential of variable va V a a(ya)
Metric Labeling Post Random variables V = {v1, v2, , vn} Label set L = {l1, l2, , lh} Labeling y Ln Labelings quantatively distinguished by energy E(y) Pairwise potential of variables (va,vb) miny a a(ya)+ (a,b) wab d(ya,yb) wab is non-negative d(.,.) is a metric distance function
Outline Post Existing Work Move-Making Algorithms (Efficient) Linear Programming Relaxation (Accurate) Rounding-based Moves Equivalence Complete Rounding and Complete Move Interval Rounding and Interval Move Hierarchical Rounding and Hierarchical Move
Expansion Algorithm Variables take label l or retain current label Post Tree Ground Initialize with Tree Expand Ground Expand House Expand Sky House Sky Boykov, Veksler and Zabih, ICCV 1999
Move-Making Algorithms Start with an initial labeling y0 Post Iteration t Define St Ln containing current labeling yt a a(ya)+ (a,b) wab d(ya,yb) argminy yt+1 = s.t. y St Above problem is easier than original problem Sometimes it can even be solved exactly
Outline Post Existing Work Move-Making Algorithms (Efficient) Linear Programming Relaxation (Accurate) Rounding-based Moves Equivalence Complete Rounding and Complete Move Interval Rounding and Interval Move Hierarchical Rounding and Hierarchical Move
Linear Programming Relaxation Binary indicator xa(i) {0,1} Post If variable a takes the label i then xa(i) = 1 i xa(i) = 1 Each variable a takes one label Similarly, binary indicator xab(i,k) {0,1} Chekuri, Khanna, Naor and Zosin, SODA 2001
Linear Programming Relaxation Minimize a linear function over feasible x Post Rounding Indicators xa(i), xab(i,k) {0,1} Relaxed xa(i), xab(i,k) [0,1] Chekuri, Khanna, Naor and Zosin, SODA 2001
Outline Post Existing Work Move-Making Algorithms (Efficient) Linear Programming Relaxation (Accurate) Rounding-based Moves Equivalence Complete Rounding and Complete Move Interval Rounding and Interval Move Hierarchical Rounding and Hierarchical Move
Move-Making Bound Post y: Estimated Labeling y*: Optimal Labeling a a(ya) + (a,b) wabd(ya,yb) a a(y*a) + (a,b) wabd(y*a,y*b)
Move-Making Bound Post y: Estimated Labeling y*: Optimal Labeling a a(ya) + (a,b) wabd(ya,yb) B a a(y*a) + (a,b) wabd(y*a,y*b) For all possible values of a(i) and wab
Rounding Approximation Post x*: LP Optimal Solution x: Rounded Solution a i a(i)xa(i) + (a,b) (i,k) wabd(i,k)xab(i,k) a i a(i)x*a(i) + (a,b) (i,k) wabd(i,k)x*ab(i,k)
Rounding Approximation Post x*: LP Optimal Solution x: Rounded Solution a i a(i)xa(i) + (a,b) (i,k) wabd(i,k)xab(i,k) A a i a(i)x*a(i) + (a,b) (i,k) wabd(i,k)x*ab(i,k) For all possible values of a(i) and wab
Equivalence Post For any known rounding with approximation A there exists a move-making algorithm such that the move-making bound B = A We know how to design such an algorithm
Outline Post Existing Work Move-Making Algorithms (Efficient) Linear Programming Relaxation (Accurate) Rounding-based Moves Equivalence Complete Rounding and Complete Move Interval Rounding and Interval Move Hierarchical Rounding and Hierarchical Move
Complete Rounding Post Treat x*a(i) [0,1] as probability that ya = li Cumulative probability za(i) = j ix*a(j) r za(2) za(i) za(k) 0 za(1) za(h) = 1 Generate a random number r (0,1] Assign the label next to r
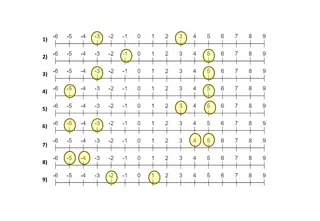
Complete Rounding - Example Post 0.5 0.25 0.75 1.0 r za(2) za(3) 0 za(1) za(4) 0.7 0.8 0.9 1.0 r zb(1) zb(3) 0 zb(4) zb(2) 0.2 0.3 0.1 1.0 r 0 zc(3) zc(2) zc(4) zc(1)
Equivalent Move Post Complete Move !!
Complete Move Post Start with an initial labeling y0 Iteration t Define St Ln a a(ya)+ (a,b) wab d(ya,yb) argminy yt+1 = s.t. y St
Complete Move Post Start with an initial labeling y0 Iteration t Define St= Ln a a(ya)+ (a,b) wab d(ya,yb) argminy yt+1 = s.t. y St Above problem is the same as the original problem How do we solve this problem?
Complete Move Post Define St= Ln a a(ya)+ (a,b) wabd (ya,yb) argminy yt+1 = s.t. y St Above problem is the same as the original problem How do we solve this problem?
Complete Move Post Define St= Ln a a(ya)+ (a,b) wabd (ya,yb) argminy yt+1 = s.t. y St Submodular overestimation d of d Obtained by solving a small LP
Submodular Overestimation Post mind maxi,k d (li,lk)/d(li,lk) d (li,lk) d(li,lk) s.t. d (li,lk+1) + d (li+1,lk) d(li,lk) + d(li+1,lk+1)
Submodular Overestimation Post mind b d (li,lk) d(li,lk) s.t. d (li,lk+1) + d (li+1,lk) d(li,lk) + d(li+1,lk+1) bd(li,lk) d (li,lk) Dual provides worst-case instance for complete rounding
Outline Post Existing Work Move-Making Algorithms (Efficient) Linear Programming Relaxation (Accurate) Rounding-based Moves Equivalence Complete Rounding and Complete Move Interval Rounding and Interval Move Hierarchical Rounding and Hierarchical Move
Interval Rounding Post Treat x*a(i) [0,1] as probability that ya = li Cumulative probability za(i) = j ix*a(j) za(2) za(i) za(k) 0 za(1) za(h) = 1 Choose an interval of length h
Interval Rounding Post Treat x*a(i) [0,1] as probability that ya = li Cumulative probability za(i) = j ix*a(j) r 0 za(k)-za(i) REPEAT Choose an interval of length h Generate a random number r (0,1] Assign the label next to r if it is within the interval
Interval Rounding - Example Post 0.25 0.5 0.75 1.0 za(2) za(3) 0 za(1) za(4) 0.7 0.8 0.9 1.0 zb(1) zb(3) 0 zb(4) zb(2) 0.2 0.3 0.1 1.0 0 zc(3) zc(2) zc(4) zc(1)
Interval Rounding - Example Post 0.25 0.5 r za(2) 0 za(1) 0.7 0.8 r zb(1) 0 zb(2) 0.2 0.1 r 0 zc(1) zc(2)
Interval Rounding - Example Post 0.25 0.5 0.75 1.0 za(2) za(3) 0 za(1) za(4) 0.7 0.8 0.9 1.0 zb(1) zb(3) 0 zb(4) zb(2) 0.2 0.3 0.1 1.0 0 zc(3) zc(2) zc(4) zc(1)
Interval Rounding - Example Post 0.2 0.3 0.1 1.0 0 zc(3) zc(2) zc(4) zc(1)
Interval Rounding - Example Post 0.1 0.2 r zc(3) zc(2) -zc(1) -zc(1) 0
Interval Rounding - Example Post 0.25 0.5 0.75 1.0 za(2) za(3) 0 za(1) za(4) 0.7 0.8 0.9 1.0 zb(1) zb(3) 0 zb(4) zb(2) 0.2 0.3 0.1 1.0 0 zc(3) zc(2) zc(4) zc(1)
Equivalent Move Post Interval Move !!
Interval Move Post Start with an initial labeling y0 Iteration t Choose an interval of labels of length h y St iff ya = yta or ya interval of labels a a(ya)+ (a,b) wab d(ya,yb) argminy yt+1 = s.t. y St How do we solve this problem?
Interval Move Post Start with an initial labeling y0 Iteration t Choose an interval of labels of length h y St iff ya = yta or ya interval of labels a a(ya)+ (a,b) wabd (ya,yb) argminy yt+1 = s.t. y St Submodular overestimation d of d
Outline Post Existing Work Move-Making Algorithms (Efficient) Linear Programming Relaxation (Accurate) Rounding-based Moves Equivalence Complete Rounding and Complete Move Interval Rounding and Interval Move Hierarchical Rounding and Hierarchical Move
Hierarchical Rounding Post L1 L2 L3 l1 l2 l3 l4 l5 l6 l7 l8 l9 Hierarchical clustering of labels (e.g. r-HST metrics)
Hierarchical Rounding Post L1 L2 L3 l1 l2 l3 l4 l5 l6 l7 l8 l9 Assign variables to labels L1, L2 or L3 Move down the hierarchy until the leaf level
Hierarchical Rounding Post L1 L2 L3 l1 l2 l3 l4 l5 l6 l7 l8 l9 Assign variables to labels l1, l2 or l3
Hierarchical Rounding Post L1 L2 L3 l1 l2 l3 l4 l5 l6 l7 l8 l9 Assign variables to labels l4, l5 or l6
Hierarchical Rounding Post L1 L2 L3 l1 l2 l3 l4 l5 l6 l7 l8 l9 Assign variables to labels l7, l8 or l9
Equivalent Move Post Hierarchical Move !!
Hierarchical Move Post L1 L2 L3 l1 l2 l3 l4 l5 l6 l7 l8 l9 Hierarchical clustering of labels (e.g. r-HST metrics)
Hierarchical Move Post L1 L2 L3 l1 l2 l3 l4 l5 l6 l7 l8 l9 Obtain labeling y1 restricted to labels {l1,l2,l3}
Hierarchical Move Post L1 L2 L3 l1 l2 l3 l4 l5 l6 l7 l8 l9 Obtain labeling y2 restricted to labels {l4,l5,l6}
Hierarchical Move Post L1 L2 L3 l1 l2 l3 l4 l5 l6 l7 l8 l9 Obtain labeling y3 restricted to labels {l7,l8,l9}
Hierarchical Move Post L1 L2 L3 y3(a) y3(b) y2(a) y2(b) y1(a) y1(b) Va Vb Move up the hierarchy until we reach the root
Questions? http://mpawankumar.info