Rounding Decimal Numbers Explained with Examples
Understand the rules of rounding decimal numbers to a given number of decimal places and learn the importance of approximations in real-life situations. Examples provided for better comprehension.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
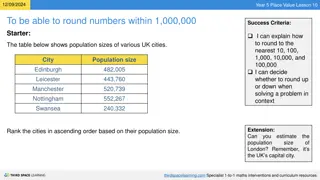
28 April 2025 Rounding decimal places and estimation LO: Write numbers rounded to a given number of decimal places. www.mathssupport.org www.mathssupport.org
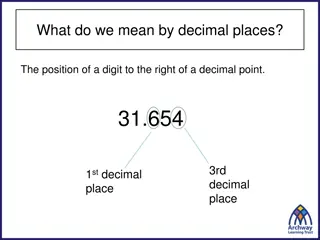
Rounding decimal places Rounding decimal numbers correct to a given number of decimal places (dp). The following rules apply when rounding numbers correct to a given number of decimal places (dp) If the digit after the one that is being rounded is less than 5 then keep the rounded digit unchanged and delete the following digits. If the digit after the one that is being rounded is 5 or more then we need to add 1 to the rounded digit and delete the following digits. www.mathssupport.org www.mathssupport.org
Rounding decimal places It is often necessary/convenient/sensible to give approximations to real life situations or as answers to certain calculations. For example The time in which an athlete runs a 100m race is given by: a) 10.1 seconds b) 10.14 seconds or c) 10 seconds. 100 Metre times need to be accurate to the nearest hundredth of a second. Hence 10.14 s is the sensible answer www.mathssupport.org www.mathssupport.org
Rounding decimal places It is often necessary/convenient/sensible to give approximations to real life situations or as answers to certain calculations. For example if a case of a drink containing 6 bottles costs 25 then you could price a single bottle by calculating 25 6 = 4.166666667. It would be pointless to write out all the numbers on your calculator display. Since we are dealing with money (pounds and pence) we only need 2 decimal places (2 d.p.) So it would be much better to write down 4.17. www.mathssupport.org www.mathssupport.org
Rounding decimal places Numbers can be rounded to 1,2, 3 or more decimal places. Rounding to 1 d.p 4 . 8 3 2 5 4. 8 5 2 5 4. 8 4 2 5 5 or bigger ? 5 or bigger ? 5 or bigger ? No No Yes 4.8 4.9 4.8 www.mathssupport.org www.mathssupport.org
Rounding decimal places Rounding to 1 d.p 4 . 8 3 2 5 4. 8 5 2 5 4. 8 4 2 5 5 or bigger ? 5 or bigger ? 5 or bigger ? No No Yes 4.8 4.9 4.8 4. 8 6 2 5 4. 8 7 2 5 4. 8 9 2 5 5 or bigger ? 5 or bigger ? 5 or bigger ? Yes Yes Yes 4.9 4.9 4.9 www.mathssupport.org www.mathssupport.org
Rounding to 2 d.p 5. 8 4 2 5 1. 4 2 6 1 0. 6 0 8 3 5 or bigger ? 5 or bigger ? 5 or bigger ? No Yes Yes 1.43 5.84 0.61 0. 2 9 4 3 0. 5 5 5 0 0. 3 9 7 0 5 or bigger ? 5 or bigger ? 5 or bigger ? Yes No Yes 0.29 0.40 0.56 www.mathssupport.org www.mathssupport.org
Rounding to 3 d.p 5. 8 4 2 5 4 1. 4 2 6 1 8 0. 6 0 8 3 4 5 or bigger ? 5 or bigger ? 5 or bigger ? Yes No No 1.426 5.843 0.608 6. 2 9 4 7 1 5. 4 0 0 9 7 0. 3 9 9 7 7 5 or bigger ? 5 or bigger ? 5 or bigger ? Yes Yes Yes 6.295 5.401 0.400 www.mathssupport.org www.mathssupport.org
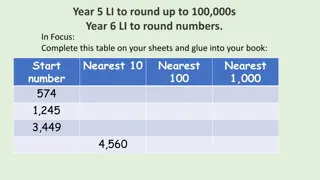
Rounding to a specified accuracy Rounding to the nearest thousand 6 0 8 3 4 4 2 5 4 8 4 2 3 1 8 5 or bigger ? 5 or bigger ? 5 or bigger ? Yes No Yes 42 000 61 000 43 000 Rounding to the nearest tens Rounding to the nearest hundred 4 0 0 9 7 3 9 9 7 7 2 9 4 7 1 5 or bigger ? 5 or bigger ? 5 or bigger ? Yes Yes Yes 29 500 40 100 39 980 www.mathssupport.org www.mathssupport.org
Estimation Martin uses his calculator to work out 39 72. The display shows an answer of 1053. How do you know this answer must be wrong? 40 70 = 2800 39 72 is approximately equal to Also, if we multiply together the last digits of 39 and 72 we have 9 2 = 18. 9 2 = 18. The product of 39 and 72 must therefore end in an 8. www.mathssupport.org www.mathssupport.org
Estimation How could we estimate the answer to 3.5 17.5? 3.5 17.5 can be approximated to: 4 20 = 80 www.mathssupport.org www.mathssupport.org
Estimation How could we estimate the answer to 5948 58? 5948 58 can be approximated to: 6000 60 = 100 www.mathssupport.org www.mathssupport.org
Thank you for using resources from A close up of a cage Description automatically generated For more resources visit our website https://www.mathssupport.org If you have a special request, drop us an email info@mathssupport.org www.mathssupport.org www.mathssupport.org