Second-Order Transients in Electrical Circuits

Slide Note

An exploration of second-order transients in electrical circuits excited by initial conditions. Learn how to analyze RLC series circuits, find natural initial conditions, determine damping cases, and obtain specific solutions. Detailed algorithms and step-by-step examples provided.

jone_iam Follow

Uploaded on Feb 21, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

Download Presentation

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

E N D

Presentation Transcript

ENEE 205 Second Order Transients Part 1: circuits excited by initial conditions

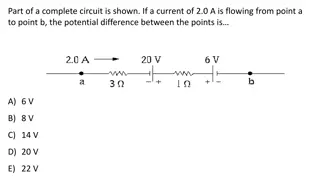
2nd-order circuits excited by initial conditions ALGORITHM: 1. Get circuit. 2. Find natural initial conditions for energy storage elements. (draw circuit for t<0 if needed). 3. Find needed initial conditions for the circuit quantity to be calculated. (draw circuit at t=0+ if needed). 4. Add a source to the circuit so that you recover the original circuit when you set the source to zero! 5. Find transfer function of desired output in terms of source (draw circuit for t>0 .) 6. Find characteristic equation by setting denominator of transfer function to zero. Determine damping case. Obtain general homogeneous solution. 7. Plug in initial conditions to the general homogeneous solution to get specific solution. (The particular solution is zero.)

RLC series circuit excited by initial conditions demonstrating Steps 4-5 to see the 3 cases t=0 Suggestion: If you have a series connection, solve for capacitor voltage first; If you have a parallel connection, solve for inductor current first. L R + Vc - Vo C 1 1 V sC = = = ( ) ; H s C t>0 + + + + 1 1 2 sL R sC s LC sRC V s L + + = characteri stic equation : 1 0 2 s LC sRC R + Vc - C ( ) 2 Vs=0 2 4 1 RC RC LC R R = = or s 2 2 2 LC L L LC 2 1 R 0 overdamped case two real roots 2 L LC 2 1 R = 0 critically damped case one real root 2 L LC 2 1 R 0 underdampe d case two complex roots 2 L LC

Critically-damped RLC series circuit t=0 1H 2W ic 2. Find natural initial conditions for energy storage elements. + Vc - 10V 1F This is a dc problem for t<0. KVL on the left mesh shows that: ??0+ = ??0 = 10 ? KVL around the outside shows that there are 10V across the resistor (no voltage across the inductor. Ohm s Law requires the resistor current be 5A, and since the resistor and inductor are in series: ??0+ = ??0 = 5 ? 3. Find needed initial conditions for the circuit quantity to be calculated. One of the needed initial conditions is also natural: ??0+ = 10 ?. We also need ??? ? ? ??=??(0+) = ??(0+) = 5 ? 1 ?= 5 ?/? =??? ?? Capacitor terminal relationship L and C are in series for t>0

Critically-damped case Steps 4 6 previously gave us: t=0 1H 2W 2 + Vc - 1 R 2 R 2 12 1 = s 10V 1F = 1 1= 1 L L LC We just need to finish the second half of step 6: Determine damping case. Obtain general homogeneous solution. Since the solutions are identical (-1), this is the critically-damped case and the general solution is always: ??, ? = ????+ ?????= ?? ?+ ??? ? 7. Plug in initial conditions to the general homogeneous solution to get specific solution. ??, 0 = 10? = ?? 0+ ? 0? 0= ? = 10? ???, 0 ?? So B=A-5=5 V/s, and ??, ? = 10? ?+ 5?? ? ? =0 =0 = 5? ? = ?? 0 ? 0? 0+ ? ? 0= ? ?

Overdamped RLC series circuit 2. Find natural initial conditions for energy storage elements. (Very similar to last case!) t=0 iL 1H 4W ic + Vc - 10V 1F This is a dc problem for t<0. KVL on the left mesh shows that: ??0+ = ??0 = 10 ? KVL around the outside shows that there are 10V across the resistor (no voltage across the inductor. Ohm s Law requires the resistor current be 2.5A, and since the resistor and inductor are in series: ??0+ = ??0 = 2.5 ? 3. Find needed initial conditions for the circuit quantity to be calculated. One of the needed initial conditions is also natural: ??0+ = 10 ?. We also need ??? ? ? ??=??(0+) = ??(0+) = 2.5 ? 1 ? = 2.5 ?/? =??? ?? Capacitor terminal relationship L and C are in series for t>0

Overdamped case Steps 4 6 previously gave us: t=0 1H 4W + Vc - 2 1 R 2 R 2 22 1 10V 1F = s = 2 1= 2 3 L L LC We just need to finish the second half of step 6: Determine damping case. Obtain general homogeneous solution. Since the solutions are real and distinct, this is the overdamped case and the general solution is always: ??, ? = ???+?+ ??? ?= ?? .268?+ ?? 3.732? 7. Plug in initial conditions to the general homogeneous solution to get specific solution. ??, 0 = 10? = ?? 0+ ?? 0= ? + ? ???, 0 ?? = 2.5? ? = ?+?? 0+ ? ?? 0= ?+? + ? ?

Overdamped case It may be best to solve this with matrices: 1 ?+ 1 ? 10 2.5 ? ? = ? 1 ? ?+ ?+ ? ?+ ? ?+ 1 ? ?+ 10 2.5 ? ? = 3.732 3.464 .268 3.464 1 10 2.5 ? ? 10.052 .052 3.464 1 3.464 = = ?

Underdamped RLC series circuit 2. Find natural initial conditions for energy storage elements. (Very similar to last two cases!) t=0 1H 1W ic 1F + Vc - 10V This is a dc problem for t<0. KVL on the left mesh shows that: ??0+ = ??0 = 10 ? KVL around the outside shows that there are 10V across the resistor (no voltage across the inductor. Ohm s Law requires the resistor current be 10 A, and since the resistor and inductor are in series: ??0+ = ??0 = 10 ? 3. Find needed initial conditions for the circuit quantity to be calculated. One of the needed initial conditions is also natural: ??0+ = 10 ?. We also need ??? ? ? ??=??(0+) = ??(0+) = 10 ? 1 ? = 10 ?/? =??? ?? Capacitor terminal relationship L and C are in series for t>0

t=0 Underdamped case Steps 4 6 previously gave us: 1H 1W + Vc - 10V 1F 2 1 R 2 R 2 = 1 0.52 1 1= 1 ? 3 = s 2 = ? ?? L L LC 2 We just need to finish the second half of step 6: Determine damping case. Obtain general homogeneous solution. Since the solutions are complex numbers, this is the underdamped case and the general solution is always: ??, ? = ?? ??cos?? + ?? ??sin?? for ? =1 3 2, = 2 7. Plug in initial conditions to the general homogeneous solution to get specific solution. ??, 0 = 10? = ?? 0cos(0) + ?? 0sin(0) = ? = 10?

Underdamped case ???, ? ?? ??? ??cos(?t) ???, 0 ?? = ??? 0cos(0) + ??? 0cos(0) ??? 0sin(0) ??? 0sin(0) = ?? ?? = 10? = ??? ??cos?? + ??? ??sin?? ??? ??sin?? + =0 =0 ? Or ?? = ?? 10 =1 2? or ? = 10 3 210 10 = 5 = 3 So: 3? 2 10 3? 2 ??, ? = 10? ?/2cos 3? ?/2sin ?

ENEE 205 Second Order Transients Part 2: circuits excited by sources

2nd-order circuits excited by sources ALGORITHM: 1. Get circuit. 2. Find natural initial conditions for energy storage elements. (draw circuit for t<0 if needed). 3. Find needed initial conditions for the circuit quantity to be calculated. (draw circuit at t=0+ if needed). 4. Find transfer function of desired output in terms of source (draw circuit for t>0 .) 5. Find characteristic equation by setting denominator of transfer function to zero. Determine damping case. Obtain general homogeneous solution. 6. Find the particular solution by inserting s=j into transfer function and solving. 7. Plug in initial condition to COMPLETE solution (general homogeneous plus particular) to get specific solution

RLC parallel circuit excited by a source demonstrating Step 4 to see the 3 cases t=0 Suggestion: If you have a series connection, solve for capacitor voltage first; If you have a parallel connection, solve for inductor current first. + Vc - IS L R C I 1 1 sL sL iL = = = ( ) ; H s L I / 1 + + + + 1 s / 1 2 sC R sL s LC R s + + = characteri stic equation : / 1 0 2 LC sL R ( ) 2 2 / / 4 1 RC 1 RC 1 L R L R LC = = or s 2 2 2 LC LC 2 1 RC 1 0 overdamped case two real roots 2 LC 2 1 RC 1 = 0 critically damped case one real root 2 LC 2 1 RC 1 0 underdampe d case two complex roots 2 LC

Critically damped RLC parallel circuit t=0 + Vc - 2. Find natural initial conditions for energy storage elements. 1/2W 1H 1A 1F iL When there are no sources connected for t<0, one can assume that all natural initial conditions are zero, so: ??0+ = ??0 = 0 ?; ??0+ = ??0 = 0 ? 3. Find needed initial conditions for the circuit quantity to be calculated: ??0+ = 0 ?;??? ??=??(0+) =??(0+) 0? 1 ?= 0? = ? ? ? Finish Step 5: Determine damping case. Obtain general homogeneous solution. 2 12 1 1 1 1 = s = 1 1= 1 2 2 RC RC LC Since the solutions are identical (-1), this is the critically-damped case and the general solution is always: ??, ? = ????+ ?????= ?? ?+ ??? ?

Critically-damped parallel RLC 6. Find the particular solution by inserting s=j into transfer ?? 1?= 1 function and solving: ? ?? = ?+1. Since the ?2??+??? ?? 1?= 1 source is dc, = , and ? 0 = ?+1= 1,?? 02??+?0? ??= 1?,?? ??,?? = 1? 7. Plug in initial condition to COMPLETE solution (general homogeneous plus particular) to get specific solution ??? = ??,?? + ??, ? = 1 + ?? ?+ ??? ? ??0 = 0? = 1 + ?? 0+ ? 0? 0= 1 + ?, ? = 1 ???? ?? = ?? ?+ ?? ? ??? ?, so ???0 = 0 = 1 + ?, ? = 1 ?? ??? = 1 ? ? ?? ?A = 1 (1 + ?)? ? A

Critically-damped simulation TCLOSE = 0 1 2 U1 L1 1H I I1 1Adc C1 1F R1 0.5 0

Overdamped RLC parallel circuit t=0 + Vc - 2. Find natural initial conditions for energy storage elements. 1/4W 1H 1A 1F iL When there are no sources connected for t<0, one can assume that all natural initial conditions are zero, so: ??0+ = ??0 = 0 ?; ??0+ = ??0 = 0 ? 3. Find needed initial conditions for the circuit quantity to be calculated: ??0+ = 0 ?;??? ??=??(0+) =??(0+) 0? 1 ?= 0? = ? ? ? Finish Step 5: Determine damping case. Obtain general homogeneous solution. 2 22 1 1 1 1 = s = 2 1= 2 3 2 2 RC RC LC Since the solutions are real and distinct, this is the overdamped case and the general solution is always: ??, ? = ???+?+ ??? ?= ?? .268?+ ?? 3.732?

Overdamped parallel RLC 6. Find the particular solution by inserting s=j into transfer ?? 1?= 1 function and solving: ? ?? = ?+1. Since the ?2??+??? ?? 1?= 1 source is dc, = , and ? 0 = ?+1= 1,?? 02??+?0? ??= 1?,?? ??,?? = 1? 7. Plug in initial condition to COMPLETE solution (general homogeneous plus particular) to get specific solution ??? = ??,?? + ??, ? = 1 + ???+?+ ??? ? ??0 = 0? = 1 + ?? 0+ ?? 0= 1 + ? + ? ???? ?? ???0 ?? = ?+???+?+ ? ??? ? = 0 = ?+??0+ ? ??0= ?+? + ? ? = 0

Overdamped parallel RLC case It may be best to solve this with matrices: 1 ?+ 1 ? 1 0 ? ? = ? 1 ? ?+ ?+ ? ?+ ? ?+ 1 ? ?+ 1 0 ? ? = 3.732 3.464 .268 3.464 1 1 0 1.077 0.077 ? ? 3.464 1 3.464 = = ?

Overdamped simulation TCLOSE = 0 1 2 U1 L1 1H I I1 1Adc C1 1F R1 0.25 0

Underdamped RLC parallel circuit t=0 + Vc - 2. Find natural initial conditions for energy storage elements. 1W 1H 1A 1F iL When there are no sources connected for t<0, one can assume that all natural initial conditions are zero, so: ??0+ = ??0 = 0 ?; ??0+ = ??0 = 0 ? 3. Find needed initial conditions for the circuit quantity to be calculated: ??0+ = 0 ?;??? ??=??(0+) =??(0+) 0? 1 ?= 0? = ? ? ? Finish Step 5: Determine damping case. Obtain general homogeneous solution. 2 2 1 1 1 = 1 1 2 1 1= 2 ? 3 = s 2 2 2 RC RC LC 2 This is the underdamped case and the general solution is always: ??, ? = ?? ??cos?? + ?? ??sin?? for ? =1 3 2, = 2

Underdamped parallel RLC 6. Find the particular solution by inserting s=j into transfer ?? 1?= 1 function and solving: ? ?? = ?+1. Since the ?2??+??? ?? 1?= 1 source is dc, = , and ? 0 = ?+1= 1,?? 02??+?0? ??= 1?,?? ??,?? = 1? 7. Plug in initial condition to COMPLETE solution (general homogeneous plus particular) to get specific solution ??? = ??,?? + ??, ? = 1 + ?? ??cos?? + ?? ??sin?? ??0 = 0? = 1 + ?? 0cos0 + ?? 0sin0 = 1 + ? ??? = ??,?? + ??, ? = 1 ? ??cos?? + ?? ??sin??

Underdamped parallel RLC case ???, ? ?? ??? ??cos(?t) ???, 0 ?? = ?? 0cos(0) + ??? 0cos(0) ??? 0sin(0) + ?? 0sin(0) = ?? + ? = 0? = ?? ??cos?? + ??? ??sin?? + ?? ??sin?? + =0 =0 ? ? = ? ?= 1 Or 3 So: 3? 2 1 3? 2 ??? = 1 ? ? 3? ? 2cos 2sin

Underdamped simulation Overshoot TCLOSE = 0 1 2 U1 L1 1H I I1 1Adc C1 1F R1 1 0

ENEE 205 Transients Part 3: Needed Initial Conditions

Finding needed initial conditions at ? = 0+ 1. Find natural initial conditions inductor currents and capacitor voltages at ? = 0 2. If you solve for an inductor current or capacitor voltage, one natural condition will also be one of the needed initial conditions. If you are solving for something else, you are on your own! 3. To find the derivative of the current or voltage at ? = 0+, you need to find the inductor voltage or capacitor current at ? = 0+. You can then use the terminal relationship for that component to find the derivative of the circuit variable. 4. If you are looking for the capacitor voltage in a series circuit or an inductor current in a parallel circuit, finding the capacitor current or inductor voltage, respectively, is straightforward. 5. Otherwise, draw the circuit right at ? = 0+. Solve this dc circuit for the needed parameter. Voltage sources act like batteries (or shorts) and current sources act like current sources (or opens).

Initial condition example t=0 1 W For t<0, there are no sources connected to the circuit, so: ??0+ = ??0 = 0 ?; ??0+ = ??0 = 0 ? 0.5 W The circuit at ? = 0+is shown to the left. The natural initial conditions are shown in yellow. KCL at the upper left node requires that 5A goes through 0.5 W + Vc - 1 H 5 A 2 F 1 W 5 A + 5 V - + 0 V - + + 0 V - 5 V - 0 A 5 A 0 A 5 A the 1 Wresistor. Ohm s Law shows that there is a 5V drop across that resistor. KVL around the center mesh is used to find ??0+ = 5 ?. KCL at the center top node is used to find ??0+ = 5 ?. Terminal relationships are used to find the other initial condition: ?? 0+ =??0+ ? = 2.5 ?/? and ?? 0+ =??0+ = 5 ?/? ?

Initial condition example For t<0, the circuit is shown to the left. It is a steady-state, dc problem, so the capacitor has infinite impedance and the inductor has zero impedance. Thus, all 5A goes through the LC series combination. Given the reference directions, ??0 = 5? and ??0 = 10?. KVL around the left mesh gives: ??0 = 10?. The circuit for ? = 0+is also shown to the left. KCL at the top left node requires that 10 A flows through the RC series pair, so ??0+ = 10 ?. Ohm s Law yields 20V across the 2 W resistor. KVL around the right mesh yields ??0+ = 10?. Then: 0+ =??0+ t=0 t=0 2 W + V + Vc - 0.5 H 5 A 5 A 0.5 F L - 2 W + VR - t<0 W + VL - iL + Vc - 5A ? = 0+ + VR =20V - 5A + VL - ??= 5? + ??= 10? - ?? = 20?/? ? 0+ =??0+ 10? ?? = 20?/? ?

ENEE 205 Second Order Transients Part 4: Example Problems

A TWO-CAPACITOR CIRCUIT EXAMPLE ??10+ = ??10 = 0 ?;??20+ = ??20 = 0 ? Since ??10+ = 0 ?, C1 shorts out all of the circuit to the right, and so 5V drops across 2 W, and so ??10+ = 2.5?, so; 0+ =??1 + Vc2 - We use nodal analysis to find the transfer function: t=0 2 W + + Vc2 - 0.5 F Vc1 - 5 V 2 W 0.5 F 2 W 0.5 ??1 ?= 5 ?/? + Vc1 - 0.5s 0.5s 0.5 2.5 A 0.5 ??1 ??2 1 + ?/2 1/2 1/2 1 + ?/2 ??1 5= 2.5 0 2+? using Kramer s Rule we get ? ? = = 2+?2 1 Setting the denominator to zero gives us ? = 2 1 or ??1, ? = ?? ?+ ?? 3? For the particular solution, ? 0 =2 3, so ??1,?? =10 3?. Solving the initial condition 10/3 5 1 1 ? ? which yields: ??1? =10 3 5 5 3 5 2? ?+ 2? 3? V = 1 3

Two capacitor simulation ??1 ??2 TCLOSE = 0 1 R1 2 U1 2 V1 5Vdc C1 0.5 C2 0.5 R3 2 R2 2 0

TWO-INDUCTOR EXAMPLE - Solve for iL2 for t>0 t=0 t=0 For t<0, L2 takes all the current (it is a short for dc), so: ??10 = 0?,??20 = 1? The circuit for t = 0+is shown to the left. KCL for the top left node shows the current through the vertical resistor is 2A. KVL around the right mesh yields 1 W 1 W + + 3 V vL1 - vL2 - 1 A L1=1 H L2=1 H t = 0+ + + + 1V - 3A VL2 2V 0+ =??20+ ??2= 1?, so ??2 Or ??2 0+ = 1 ?/?. The transfer function can come from the current divider rule: 1 ? + 1 1 +1 ?+ 1A 0A 2A ? - - t > 0 1/(s+1) ??2 3 ? 1/s ? ? = = = 3A 1 1 ?2+ 3? + 1 ? + 1 ??2

Solve for iL2 for t>0 To find the homogeneous solution, set the denominator to zero: ?2+ 3? + 1 = 0,?? ? = 3 5 2 ??2, ? = ?? .382?+ ?? 2.618? The particular solution comes from H(j )=H(0)=0! So the particular solution is zero for this case. So ??2? = ?? .382?+ ?? 2.618? Plugging in the initial conditions: ??20+ = 1? = ? + ? 0+ = 1? ?= .382? 2.618? 1 1 .382 2.618 ? ? .171 ??2? = 1.618? .382? 0.618? 2.618?? or ?+= .382 ??? ? = 2.618 ??2 ? ? 1 1 = 1.171 .447 .447 1 1 =

2nd-order Sinusoidal source example Find vc(t) for t>0 For t<0, no sources are connected to the surface, so: ??0+ = 0 ?; ??0+ = 0 ? For ? = 0+, the capacitor shorts the circuit, so there is 1V across the Ohm resistor, so 2A flows through that resistor and into the capacitor, so ??0+ = 2? and ?? 0+ = 2? We can get the transfer function via the current divider rule: 1/2 W 2 W t=0 + cos(2t) V 1 F 1 H vc(t) - ? 2 + ? 2A 1 2 s ?? ?? 2=? ?? ? ?(2 + ?) 2 + ?2+ 1 ??? = = = 1 2 2 + ? + 2 + ? ?? 1= 2(2 + ?) 2 + ?2+ 1 ? ? =

2nd-order Sinusoidal source example Find vc(t) for t>0 1/2 W 2 W t=0 Homogeneous solution: 2 + ?2+ 1 = 0 So ? = 2 ?: underdamped with ??, ? = ?? 2?cos ? + ?? 2?sin ? + cos(2t) V 1 F 1 H vc(t) - Particular solution: ?? 1= =36 28? 2(2 + 2?) 2 + 2?2+ 1= and ??,?? =36 4(1 + ?) 4 1 + ?2+ 1=4(1 + ?) 65cos 2? +28 ? ?? = ? 2? = 8? + 1 So ??=4 1+? 1 8? Then: ??? =36 ??0 = 0 =36 So ? = 36 65sin 2? 65 65 65cos 2? +28 65cos 0 +28 65V 65sin 2? + ?? 2?cos ? + ?? 2?sin ? 65sin 0 + ?? 0cos 0 + ?? 0sin 0

2nd-order Sinusoidal source example ??? =36 65cos 2? +28 65sin 2? 36 65? 2?cos ? + ?? 2?sin ? ?? ? = 72 65sin 2? +56 65cos 2? +72 65? 2?cos ? +36 65? 2?sin ? 2?? 2?sin ? + ?? 2???? ? So ?? 0 = 2 =56 65+72 65+ ?; ? =130 128 2 65 = 65 So ??? =36 65cos 2? +28 65sin 2? 36 2 65? 2?sin ? V 65? 2?cos ? + Analytic result for capacitor voltage 0.8 0.6 0.4 0.2 0 0 2 4 6 8 10 -0.2 -0.4 -0.6 -0.8