Similarity in Right Triangles

Relationships in similar right triangles when drawing altitudes to the hypotenuse. Identify the three similar triangles formed and learn about the Geometric Mean concept in proportions.

• Geometry
• Similar Triangles
• Right Triangle
• Proportions
• Altitude

perreira_n Follow

Uploaded on Feb 16, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

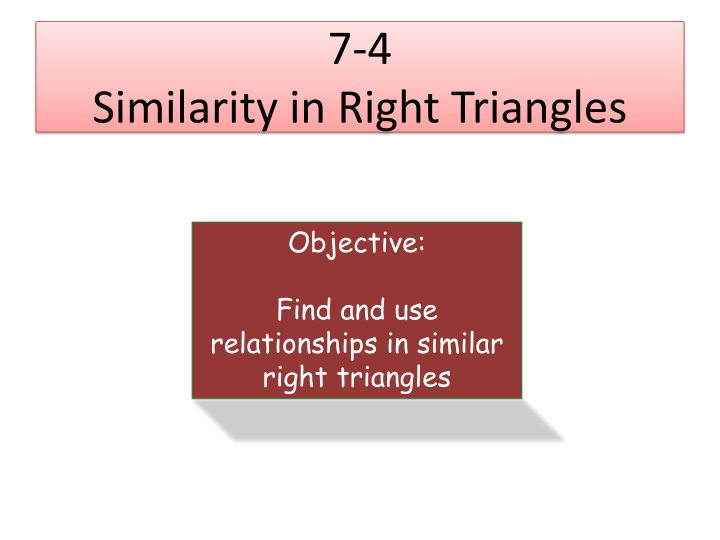
1. 7-4 Similarity in Right Triangles Objective: Find and use relationships in similar right triangles

2. When you draw the altitude to the hypotenuse of a right triangle, you form three pairs of similar right triangles.

3. What similarity statement can you write relating the three triangles in the diagram? is the altitude to the hypotenuse of right , so you can use Theorem 7-3. There are three similar triangles.

4. REMINDER: The middle two numbers in a proportion are the means. What is the Geometric Mean of 6 and 15?

7. 7-4 p. 465: 9-21 odd