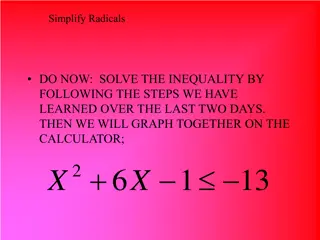Simplifying Radical Expressions Guide
Learn how to simplify radical expressions with step-by-step examples and techniques such as finding prime factorization and using perfect square factors. Improve your understanding of radicals in mathematics.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
10.2 a Simplifying Radicals Who uses this? Forest, conservation and logging workers Economists Actuary Statistician Engineer Insurance underwriters
Vocabulary a radical symbol radicand the number underneath the radical radical expression An expression that has radicals in it
Ways to Simplify A Radical Expression Option 1 Find the prime factorization of the radicand Every 2 equal factors under the radical sign is equivalent to one of those factors outside of the radical
Examples 75 = 3 5 5 = 5 3 2 5 3 = = = 2 2 3 5 5 300 10 3 = = 2 2 3 5 2 15 60 = = = 8 4 2 2 4 2 4 2 2
Ways to Simplify A Radical Expression Option 2 Express the radicand using perfect square factors Use the Product Property of Square Roots to simplify
Examples = = 75 5 3 25 3 = 25 3 = = = 300 100 3 10 3 100 3 = = 2 15 = 4 15 4 15 60 = = 4 2 8 = = 4 2 2 4 4 4 2 2
Examples = = 20 2 5 = 2 10 4 5 = = = 9 5 15 3 45 3 5 = = = 18 2 3 36 2 3 72 12 3 6 ( ) 42 35 = 14 315 = 14 9 35 = 7 15 2 21
Examples 3x 2 4 x y x x x x x y y y y 1 x 2 x xy 5 9 x y 4 6 16x y y x x x x x y y y y y y y y y 2 3 x 4 4 2 y y x x
Examples 3 3 5 15 x x 9 48x 2 2 2 2 3 x x x x x x x x 4 3 75x 3 5 3 5 x x x x 4 4 3 x x 2 15 x 3
Examples 2 5 3 12 2 20 x x 7 6 240x 6 2 2 2 2 5 3 x x x x x x 3 15 24 x x